/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 7281425

Dodaj do ulubionych
Dodaj do rozwiązanych

Na okręgu wybrano takich pięć różnych punktów: 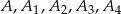A ,A 1,A 2,A 3,A 4 , że

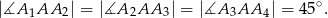
|∡A 1AA 2| = |∡A 2AA 3| = |∡A 3AA 4| = 45∘.

Udowodnij, że punkty 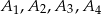A 1,A 2,A 3,A 4 są wierzchołkami kwadratu.

Rozwiązanie

PIC

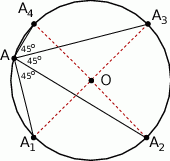
Ponieważ kąt wpisany jest połową kąta środkowego opartego na tej samej cięciwie mamy

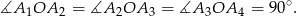
∡A 1OA 2 = ∡A 2OA 3 = ∡A 3OA 4 = 9 0∘.

W takim razie również 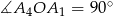∡A 4OA 1 = 90∘ , co oznacza, że czworokąt 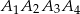A 1A 2A 3A4 ma równe wszystkie boki. Czworokąt ten ma też równe przekątne, więc jest kwadratem.

Wersja PDF