/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 7383508

Dodaj do ulubionych
Dodaj do rozwiązanych

W półkolu o o średnicy 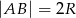|AB | = 2R narysowano dwa przystające i zewnętrznie styczne półkola 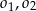o 1,o 2 , których środki leżą na odcinku 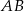AB , i które są wewnętrznie styczne do półkola o . Oblicz promień okręgu 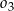o3 , który jest styczny do 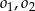o ,o 1 2 i o .

PIC

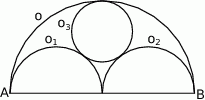
Rozwiązanie

Dorysujmy środki półkol i oznaczmy szukany promień okręgu 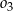o3 przez r .

PIC

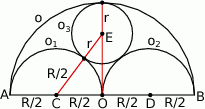
Z podanych informacji o stycznościach, możemy łatwo obliczyć długości boków trójkąta prostokątnego 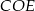COE .

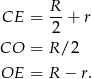
CE = R- + r 2 CO = R /2 OE = R − r.

Piszemy teraz twierdzenie Pitagorasa w tym trójkącie.

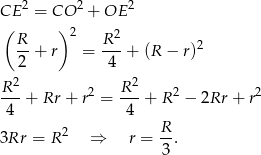
2 2 2 CE = CO + OE ( R ) 2 R 2 -- + r = ---+ (R − r)2 2 4 R 2 R2 ---+ Rr + r2 = ---+ R 2 − 2Rr + r2 4 4 3Rr = R 2 ⇒ r = R-. 3

 
Odpowiedź: R3

Wersja PDF