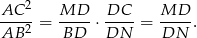Zadanie nr 7950675
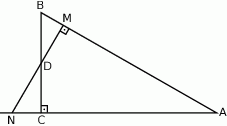
Przez środek 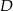 przyprostokątnej
przyprostokątnej 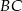 trójkąta prostokątnego
trójkąta prostokątnego 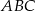 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 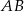 . Prosta ta przecina proste
. Prosta ta przecina proste 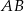 i
i 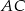 odpowiednio w punktach
odpowiednio w punktach 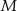 i
i 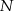 . Wykaż, że
. Wykaż, że 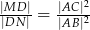 .
.
Rozwiązanie
Zauważmy, że każdy z trójkątów 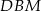 i
i 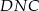 ma takie same kąty jak trójkąt
ma takie same kąty jak trójkąt 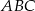 .
.
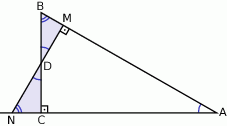
Trójkąty te są więc podobne. Z podobieństwa trójkątów 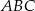 i
i 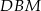 mamy
mamy
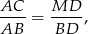
a z podobieństwa trójkątów 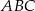 i
i 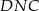 mamy
mamy
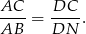
Mnożymy te równości stronami i korzystamy z tego, że punkt  jest środkiem boku BC.
jest środkiem boku BC.