Zadanie nr 8850812

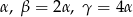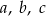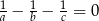Kąty w trójkącie mają miary: α, β = 2α, γ = 4α . Wykaż, że długości boków a, b, c tego trójkąta spełniają równość: 1a − 1b − 1c = 0 .

Rozwiązanie

Szkicujemy trójkąt.

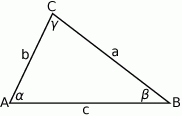
Korzystając z twierdzenia sinusów możemy zamienić długości odcinków na sinusy odpowiednich kątów. Dokładniej

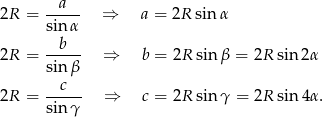
2R = --a-- ⇒ a = 2R sin α sinα --b-- 2R = sinβ ⇒ b = 2R sin β = 2R sin 2α c 2R = ----- ⇒ c = 2R sin γ = 2R sin 4α. sinγ

Musimy zatem wykazać, że

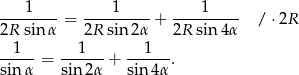
1 1 1 --------= --------- + --------- / ⋅2R 2R sin α 2R sin 2α 2R sin 4α -1--- --1--- --1--- sin α = sin2α + sin4α .

Przekształcamy prawą stronę tej równości (korzystamy ze wzoru na sumę sinusów)

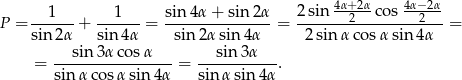
1 1 sin4 α+ sin 2α 2sin 4α+22α-cos 4α−22α- P = ------+ ------= ---------------= -------------------- = sin 2α sin 4α sin 2αsin 4α 2 sin α cosα sin4α = --sin-3αco-sα----= ---sin3α---. sin α cosα sin4 α sin αsin 4α

Zauważmy teraz, że 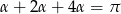α + 2α + 4α = π , więc 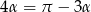4α = π − 3α , czyli 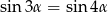sin 3α = sin 4α . W takim razie rzeczywiście

--sin3-α--- --1-- P = sin α sin 4α = sinα = L