Zadanie nr 9467250
Prosta 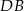 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 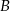 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 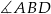 jeśli
jeśli 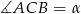 .
.
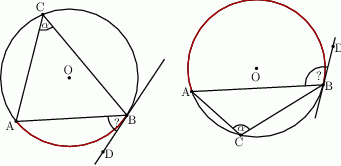
Rozwiązanie
Dorysujmy promienie 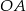 i
i 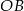 .
.
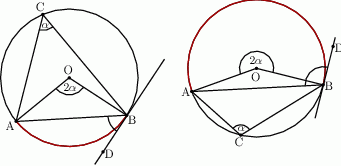
Jeżeli kąt  jest ostry (lewy rysunek), to
jest ostry (lewy rysunek), to 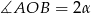 (kąt środkowy oparty na tym samym łuku, co kat wpisany
(kąt środkowy oparty na tym samym łuku, co kat wpisany 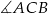 ). Zatem
). Zatem
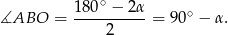
Promień 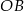 jest prostopadły do stycznej
jest prostopadły do stycznej 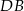 , czyli
, czyli
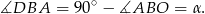
Podobnie liczymy, gdy kąt  jest rozwarty (prawy rysunek). Wtedy kąt wklęsły
jest rozwarty (prawy rysunek). Wtedy kąt wklęsły 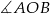 ma miarę
ma miarę 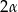 , czyli kąt wypukły
, czyli kąt wypukły 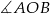 ma miarę
ma miarę 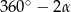 . To oznacza, że
. To oznacza, że
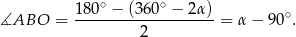
W takim razie
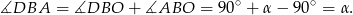
Odpowiedź: 

