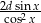Zadanie nr 9582770
Ramiona kąta ostrego o mierze 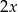 przecięto prostą
przecięto prostą  prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 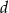 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 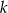 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Rozwiązanie
Zaczynamy od rysunku.
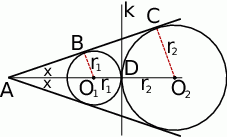
Ponieważ okręgi te są styczne zewnętrznie (bo oba są styczne do prostej 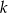 w punkcie leżącym na dwusiecznej danego kąta) to odległość ich środków jest równa sumie
w punkcie leżącym na dwusiecznej danego kąta) to odległość ich środków jest równa sumie 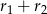 ich promieni. Z trójkątów
ich promieni. Z trójkątów 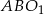 i
i 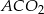 mamy
mamy
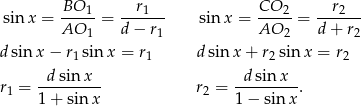
Stąd
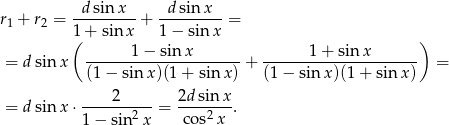
Odpowiedź: