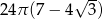Zadanie nr 9594504
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
Rozwiązanie
Oznaczmy bok wpisanego kwadratu przez  .
.
Sposób I
Naszkicujmy opisaną sytuację i dorysujmy wysokość 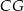 trójkąta
trójkąta  .
.
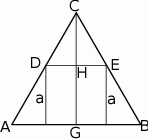
Jeżeli przez 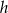 oznaczymy wysokość trójkąta równobocznego
oznaczymy wysokość trójkąta równobocznego 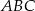 , to z podobieństwa trójkątów
, to z podobieństwa trójkątów 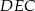 i
i 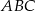 mamy
mamy
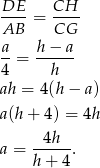
Pozostało skorzystać ze znanego wzoru 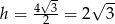 .
.
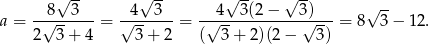
Zatem pole kwadratu jest równe
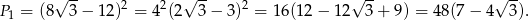
Promień  koła opisanego na kwadracie jest równy połowie przekątnej kwadratu, więc
koła opisanego na kwadracie jest równy połowie przekątnej kwadratu, więc
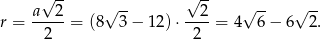
Pole koła jest równe
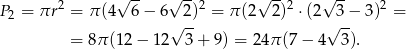
Pole koła mogliśmy obliczyć odrobinę szybciej, korzystając z obserwacji:
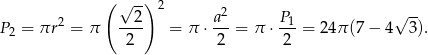
Sposób II
Tym razem również zacznijmy od rysunku i oznaczmy długość odcinka  przez
przez  .
.
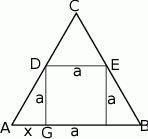
Ponieważ 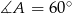 , mamy
, mamy
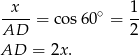
Stosujemy teraz twierdzenie Pitagorasa do trójkąta 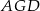
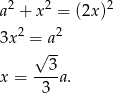
Z drugiej strony 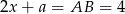 , zatem
, zatem
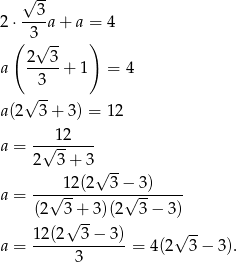
Pola wyliczamy jak w poprzednim sposobie.
Odpowiedź: 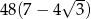 i
i