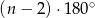/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 9684359

Dodaj do ulubionych
Dodaj do rozwiązanych
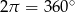  • Uzasadnij, że suma skierowanych kątów zewnętrznych dowolnego wielokąta (niekoniecznie wypukłego) jest równa 2π = 36 0∘ .
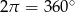  • Uzasadnij, że suma nieskierowanych kątów zewnętrznych dowolnego wielokąta wypukłego jest równa ∘ 2π = 36 0 .
  • Wyprowadź wzór na sumę kątów wewnętrznych dowolnego n –kąta.

Rozwiązanie

  • Zanim uzasadnimy podaną równość, musimy przypomnieć jak definiuje się skierowane kąty zewnętrzne.

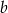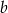    Powiedzmy że a i b są kolejnymi bokami wielokąta o wspólnym wierzchołku v (kolejnymi przy standardowej orientacji na płaszczyźnie, czyli gdy poruszamy się po brzegu wielokąta przeciwnie niż wskazówki zegara). Kąt zewnętrzny między bokami a i b jest to kąt skierowany o wierzchołku w v i początkowym ramieniu będącym przedłużeniem boku a poza v , oraz końcowym ramieniu zawierającym b .

    PIC

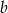    Powyższa definicja jest wprawdzie dość niezręczna, ale ma bardzo prostą interpretację geometryczną: kąt zewnętrzny mierzy o jaki kąt obrócił się bok a po przejściu przez wierzchołek v . Jeżeli kąt wewnętrzny przy wierzchołku v jest wypukły, to obracamy się o kąt nieujemny. Jeżeli natomiast kąt ten jest wklęsły, to obracamy się o kąt ujemny (w prawo).

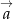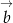    Jeżeli kogoś razi niezręczność powyższej definicji, to można łatwo ten problem rozwiązać używając wektorów: jeżeli myślimy o kolejnych bokach wielokąta jak o wektorach → a i → b , których zwrot jest wyznaczony przez dodatnią orientację brzegu wielokąta, to kąt zewnętrzny w wierzchołku v definiujemy jako kąt między wektorami → → ∡ (a, b) .

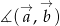    No dobrze, możemy teraz uzasadnić podaną równość.

    Wiemy już, że kąt zewnętrzny mierzy o ile obraca się bok po przejściu przez wierzchołek.

    PIC

    Zatem jadąc wzdłuż brzegu wielokąta, suma kątów zewnętrznych mierzy o ile bierzący bok jest obrócony względem boku od którego zaczęliśmy (mierzy ze znakami, więc obroty w lewo i w prawo się znoszą). Jaką sumę otrzymamy po powrocie do punktu wyjścia? – bok wróci na swoje miejsce, ale po drodze wykonał on jeden dodatni obrót o 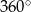∘ 360 . Daje to nam żądaną sumę kątów zewnętrznych: 360∘ .

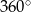    Podobnie jak w przypadku definicji, powyższa argumentacja robi się odrobinę porządniejsza jeżeli używamy wektorów. Jeżeli myślimy o bokach wielokąta jak o wektorach, to jest jasne, że obejściu brzegu wielokąta wyjściowy wektor obróci się o 360∘ .

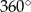    Gdyby chcieć zapisać to rozumowanie jeszcze porządniej, to musielibyśmy porządnie zdefiniować wielokąt, a tego nie chcemy robić.

  • Jak już wcześniej zauważyliśmy, w przypadku kąta wypukłego, kąt zewnętrzny jest dodatni i jego miara to dokładnie miara nieskierowanego kąta zewnętrznego. Teza wynika więc z poprzedniego podpunktu.
  • Gdyby wielokąt był wypukły, to zadanie było by bardzo proste – wystarczy wielokąt podzielić na 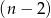(n − 2 ) trójkątów – można to zrobić prowadząc wszystkie przekątne z któregoś wierzchołka.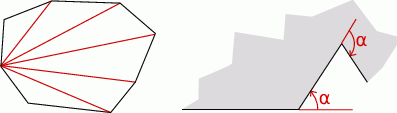
    PIC

    My chcemy jednak wyprowadzić wzór w sytuacji ogólnej, bez założenia wypukłości. Aby to zrobić, skorzystamy z obliczonej wcześniej sumy kątów zewnętrznych wielokąta.

    Zacznijmy od ustalenia jaki jest związek między miarą zorientowanego kąta zewnętrznego, a miarą niezorientowanego kąta wewnętrznego. Jeżeli kąt zewnętrzny ma miarę 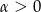α > 0 , to odpowiadający kąt wewnętrzny ma miarę 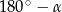∘ 18 0 − α . Jeżeli natomiast kąt zewnętrzny ma miarę 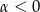α < 0 , to z rysunku łatwo odczytać, że kąt wewnętrzny będzie miał miarę 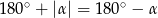180∘ + |α| = 180∘ − α (przy czym α jest teraz ujemne!).

    Zatem suma kątów wewnętrznych n –kąta to dokładnie

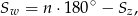
    Sw = n ⋅180∘ − Sz,

    gdzie przez 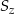Sz oznaczyliśmy sumę kątów zewnętrznych. Zatem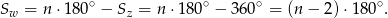

    Sw = n ⋅180∘ − Sz = n ⋅1 80∘ − 360∘ = (n − 2 )⋅180 ∘.

     
    Odpowiedź: (n − 2) ⋅180∘

Wersja PDF