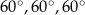/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 9827823

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.

Rozwiązanie

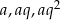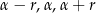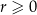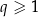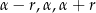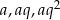Oznaczmy długości boków trójkąta przez 2 a,aq,aq , a miary kątów przez α − r,α,α + r , gdzie r ≥ 0 i q ≥ 1 . Korzystając z tego, że w trójkącie naprzeciwko większego kąta leży dłuższy bok, kąty α − r,α ,α+ r leżą naprzeciwko odpowiednio boków a,aq,aq 2 .

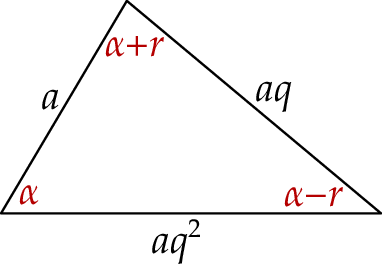
ZINFO-FIGURE

Ponieważ suma kątów w trójkącie wynosi 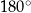18 0∘ mamy

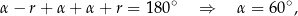
α − r+ α + α + r = 180∘ ⇒ α = 60∘,

czyli kąty mają miary 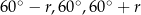60∘ − r,60∘,60∘ + r . Piszemy teraz twierdzenie cosinusów dla kąta 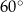60∘ i obliczamy q .

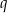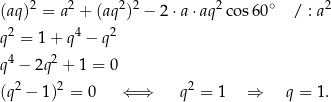
(aq)2 = a 2 + (aq2)2 − 2 ⋅a⋅ aq2cos 60∘ / : a2 q2 = 1 + q4 − q2 4 2 q − 2q + 1 = 0 (q2 − 1)2 = 0 ⇐ ⇒ q2 = 1 ⇒ q = 1.

Zatem trójkąt jest równoboczny.  
Odpowiedź: ∘ ∘ ∘ 60 ,6 0 ,60

Wersja PDF