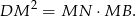Zadanie nr 9930402
Punkt 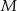 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 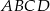 . Punkt
. Punkt 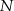 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 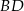 i wysokości
i wysokości 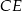 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 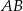 . Wykaż, że
. Wykaż, że 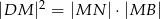 .
.
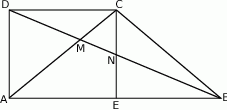
Rozwiązanie
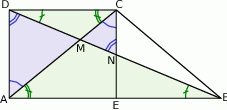
Zauważmy, że mamy dwie pary podobnych trójkątów 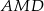 i
i 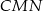 , oraz
, oraz 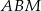 i
i  (podobieństwo wynika z równości zaznaczonych kątów).
(podobieństwo wynika z równości zaznaczonych kątów).
Z pierwszego podobieństwa mamy
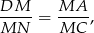
a z drugiego
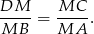
Mnożąc te dwie równości stronami mamy
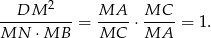
Zatem rzeczywiście