Zadanie nr 5352225
W trójkącie równoramiennym 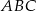 , w którym
, w którym 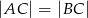 wysokość
wysokość 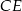 jest dwa razy dłuższa od wysokości
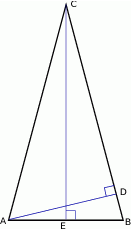
jest dwa razy dłuższa od wysokości 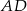 (patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta
(patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta 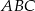 .
.
Rozwiązanie
Ogólnie, to to co chcemy zrobić, to zamienić podaną informację o stosunku wysokości na informację o stosunku boków trójkąta – bo to, mniej więcej, daje funkcje trygonometryczne jego kątów. Najważniejsze to znaleźć jakąś równość w danym trójkącie, w której występują jednocześnie obie wysokości. Możliwości jest wiele, ale dwie najprostsze to
- dwa wzory na pole:
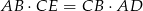 ,
, - podobieństwo trójkątów
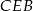 i
i 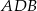 :
: 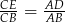 .
.
Każda z tych równości prowadzi do wniosku
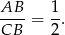
I to w zasadzie prawie koniec, zostało jeszcze sporo rachunków, ale są one dość oczywiste – jest już jasne, że kształt (a więc kąty) trójkąta 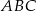 jest przez ten warunek jednoznacznie wyznaczony (z warunku z wysokościami nie było to całkiem jasne).
jest przez ten warunek jednoznacznie wyznaczony (z warunku z wysokościami nie było to całkiem jasne).
No to liczymy. Najpierw 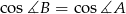 :
:
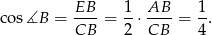
Na wyliczenie 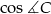 znowu jest wiele różnych sposobów, ale najmniej trickowy to wyliczenie
znowu jest wiele różnych sposobów, ale najmniej trickowy to wyliczenie 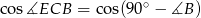 , a potem ze wzoru
, a potem ze wzoru 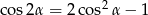 . Liczymy:
. Liczymy:
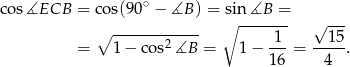
I dalej
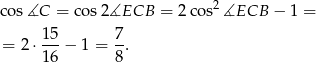
Odpowiedź: 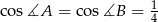 ,
,