/Konkursy/Zadania/Geometria/Planimetria/Trójkąt

Zadanie nr 9078651

Dodaj do ulubionych
Dodaj do rozwiązanych

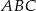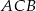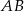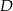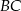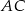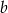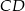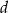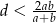W trójkacie ABC dwusieczna kąta ACB przecina bok AB w punkcie D . Długosci boków BC i AC są równe odpowiednio a i b , a długość odcinka CD jest równa d . Wykaż, że d < 2ab- a+b .

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

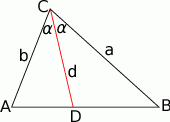
Korzystamy ze wzoru na pole trójkąta z sinusem.

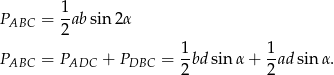
PABC = 1-absin 2α 2 1- 1- PABC = PADC + PDBC = 2bd sinα + 2ad sin α.

Jeżeli dołożymy do tego równość 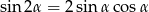sin 2α = 2sin αcos α to mamy

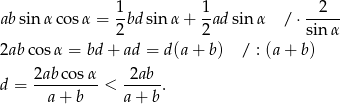
absin αcos α = 1bd sin α + 1-adsin α / ⋅--2-- 2 2 sin α 2abco sα = bd + ad = d(a + b) / : (a+ b) d = 2ab-cos-α < 2ab--. a + b a+ b

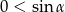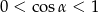Po drodze korzystaliśmy z tego, że 0 < sin α i 0 < cos α < 1 .

Wersja PDF