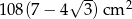Zadanie nr 9169709
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Rozwiązanie
Oznaczmy bok wpisanego kwadratu przez  .
.
Sposób I
Naszkicujmy opisaną sytuację i dorysujmy wysokość 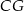 trójkąta
trójkąta 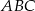 .
.
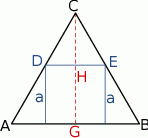
Jeżeli przez 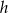 oznaczymy wysokość trójkąta równobocznego
oznaczymy wysokość trójkąta równobocznego  , to z podobieństwa trójkątów
, to z podobieństwa trójkątów 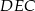 i
i 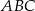 mamy
mamy
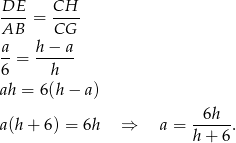
Pozostało skorzystać ze znanego wzoru 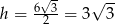 .
.
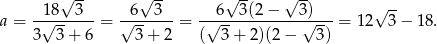
Zatem pole kwadratu jest równe
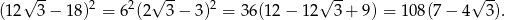
Sposób II
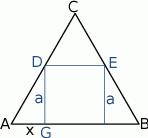
Tym razem również zacznijmy od rysunku i oznaczmy długość odcinka 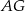 przez
przez  .
.
Mamy zatem
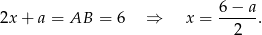
Patrzymy teraz na trójkąt prostokątny 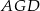 .
.
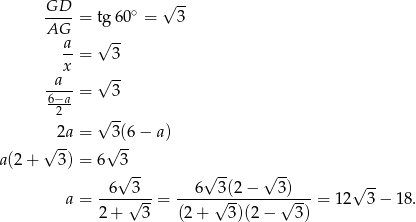
Pole liczymy tak samo jak w pierwszym sposobie.
Sposób III
Używamy oznaczeń wprowadzonych w sposobie II. Ponieważ 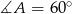 , mamy
, mamy
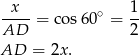
Stosujemy teraz twierdzenie Pitagorasa do trójkąta 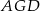
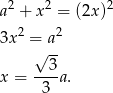
Z drugiej strony 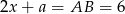 , zatem
, zatem
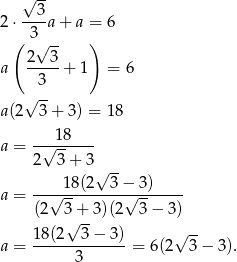
Pole obliczamy tak jak w pierwszym sposobie.
Odpowiedź: