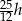/Konkursy/Zadania/Geometria/Planimetria/Trójkąt

Zadanie nr 9487501

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość trójkąta prostokątnego poprowadzona do przeciwprostokątnej ma długość 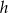h i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.

Rozwiązanie

Sposób I

PIC

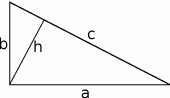
Wiemy że 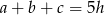a+ b+ c = 5h . Ponadto ze wzorów na pole trójkąta

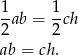
1 1 2ab = 2ch ab = ch.

Mamy zatem trzy równania na 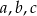a,b,c (trzecie to twierdzenie Pitagorasa) i chcemy te liczby wyliczyć. Można to zrobić na różne sposoby, ale najprostszy jest następujący

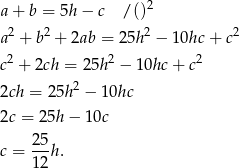
a+ b = 5h − c / ()2 2 2 2 2 a + b + 2ab = 25h − 10hc + c c2 + 2ch = 25h2 − 10hc + c2 2ch = 25h 2 − 1 0hc 2c = 25h − 10c c = 25-h. 12

Stąd

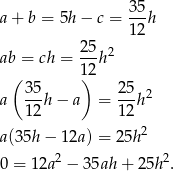
35 a + b = 5h − c = --h 12 ab = ch = 25-h2 ( 1)2 3 5 25 2 a ---h − a = ---h 1 2 12 a(35h − 1 2a) = 25h2 2 2 0 = 12a − 3 5ah + 25h .

Dalej 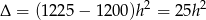Δ = (1 225− 1200)h2 = 25h2 ,

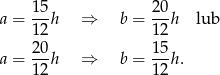
1 5 20 a = ---h ⇒ b = --h lub 1 2 12 2-0 15- a = 1 2h ⇒ b = 12h.

Sposób II

Zaczynamy od rysunku.

PIC

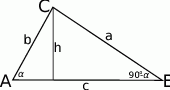
Wiemy, że 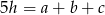5h = a + b + c . Korzystając z tego warunku, spróbujemy wyliczyć kąty trójkąta 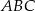ABC . Mamy

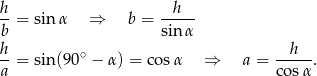
h h --= sinα ⇒ b = ----- b sin α h-= sin(90∘ − α) = cosα ⇒ a = --h--. a cos α

Ponadto, ze wzoru na pole

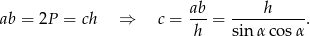
ab = 2P = ch ⇒ c = ab-= ----h-----. h sin α cosα

Mamy zatem

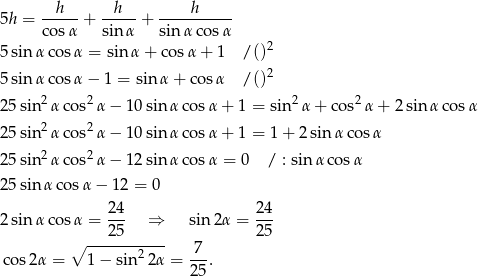
5h = --h-- + --h-- + ----h----- cos α sin α sinα cos α 5 sin α cosα = sinα + co sα + 1 / ()2 2 5 sin α cosα − 1 = sin α + co sα / () 25 sin2α cos2 α− 10sin αcos α + 1 = sin2 α+ cos2α + 2 sin α cosα 25 sin2α cos2 α− 10sin αcos α + 1 = 1 + 2 sin α cosα 2 2 25 sin α cos α− 12sin αcos α = 0 / : sinα cos α 25 sinα cos α− 12 = 0 24 24 2 sin α cosα = --- ⇒ sin 2α = --- ∘ ---25------ 25 2 -7- cos2α = 1 − sin 2 α = 25 .

Funkcje kąta α wyliczamy ze wzoru

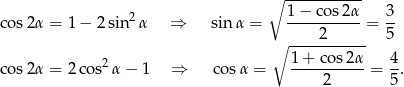
∘ ----------- cos2α = 1− 2sin2 α ⇒ sin α = 1−--cos2α- = 3- ∘ ----2------ 5 1 + cos 2α 4 cos2α = 2co s2α − 1 ⇒ cosα = ---------- = -. 2 5

Zatem

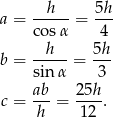
h 5h a = -----= --- cosα 4 b = -h---= 5h- sin α 3 ab 25h c = ---= ---. h 12

 
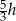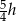Odpowiedź: 5 3h , 5 4h , 25 12h

Wersja PDF