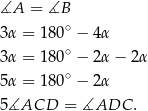Zadanie nr 9507635
Punkt 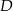 leży na boku
leży na boku 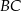 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 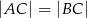 . Odcinek
. Odcinek 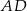 dzieli trójkąt
dzieli trójkąt 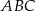 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 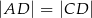 i
i 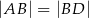 . Wykaż, że
. Wykaż, że 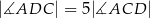 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
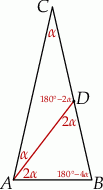
Oznaczmy 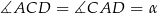 . Wtedy
. Wtedy
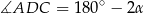
i
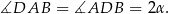
Stąd
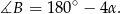
Teraz pozostało skorzystać z tego, że trójkąt 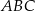 jest równoramienny.
jest równoramienny.