Zadanie nr 9817352
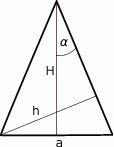
W trójkącie równoramiennym (patrz rysunek) długość podstawy wynosi  , zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe
, zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe 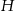 i
i 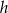 . Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę
. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę  .
.
- Wyraź
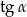 w zależności od wielkości
w zależności od wielkości  i
i 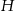 .
. - Wyraź
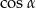 w zależności od wielkości
w zależności od wielkości  i
i 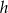 .
. - Wykaż, że jeśli
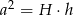 , to
, to 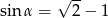 .
.
Rozwiązanie
- W zasadzie nie ma co objaśniać, wystarczy pamiętać co to jest
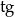 :
: 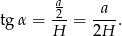
Odpowiedź: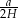
- Ponieważ wysokości są prostopadłe do boków, to
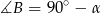 (rysunek).
(rysunek). 
Stąd
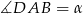 . Wyliczamy teraz z trójkąta
. Wyliczamy teraz z trójkąta 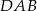 :
: 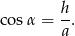
Odpowiedź: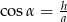
- Na początek nie przejmujmy się podanym warunkiem (bo nie bardzo wiadomo co z nim zrobić) i spróbujmy wyliczyć
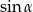 . Jeżeli oznaczymy
. Jeżeli oznaczymy 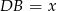 (rysunek), to
(rysunek), to 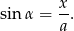
Musimy zatem wyliczyć
 – możemy to zrobić z podobieństwa dwóch zaznaczonych trójkątów prostokątnych (tych z kątem
– możemy to zrobić z podobieństwa dwóch zaznaczonych trójkątów prostokątnych (tych z kątem  ). Mamy
). Mamy 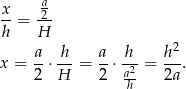
Skorzystaliśmy oczywiście z równości
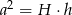 . Teraz jest najbardziej ’trickowy’ krok. Z otrzymanego równania nie uda nam się wprost wyliczyć
. Teraz jest najbardziej ’trickowy’ krok. Z otrzymanego równania nie uda nam się wprost wyliczyć  (podane warunki wyznaczają trójkąt tylko z dokładnością do podobieństwa), ale my nie mamy wyliczyć
(podane warunki wyznaczają trójkąt tylko z dokładnością do podobieństwa), ale my nie mamy wyliczyć  -a tylko
-a tylko 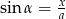 . Mając to na uwadze przekształcamy:
. Mając to na uwadze przekształcamy: 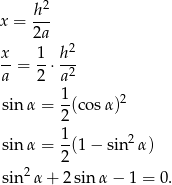
No i teraz powinno być już łatwo, po podstawieniu
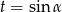 mamy zwykłe równanie kwadratowe.
mamy zwykłe równanie kwadratowe. 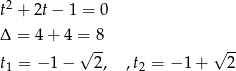
Pierwsza z tych liczb jest mniejsza od -1, nie może więc być wartością
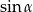 . Wykazalismy zatem, że
. Wykazalismy zatem, że 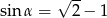 .
.

