Zadanie nr 9309271
W trójkącie 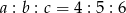 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 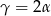 .
.
Rozwiązanie
Zaczynamy od rysunku.
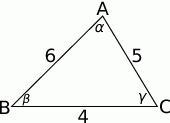
Ponieważ interesują nas tylko kąty trójkąta, a nie jego rozmiar, możemy przyjąć, że boki trójkąta mają długości 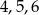 (jak ktoś nie wierzy, że tak można, to może sobie przyjąć
(jak ktoś nie wierzy, że tak można, to może sobie przyjąć 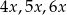 i zobaczyć, że
i zobaczyć, że  się później skróci). Z twierdznia cosinusów wyliczymy
się później skróci). Z twierdznia cosinusów wyliczymy 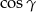 i
i 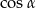 . Potem wystarczy zauważyć, że
. Potem wystarczy zauważyć, że
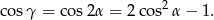
Najpierw liczymy 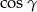 .
.
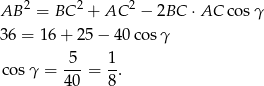
Teraz liczymy 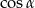 .
.
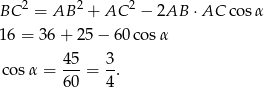
Zatem
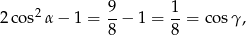
czyli 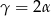 .
.

