Zadanie nr 1883292
Wyznacz zbiór wartości funkcji 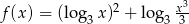 zdefiniowanej na przedziale
zdefiniowanej na przedziale 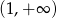 .
.
Rozwiązanie
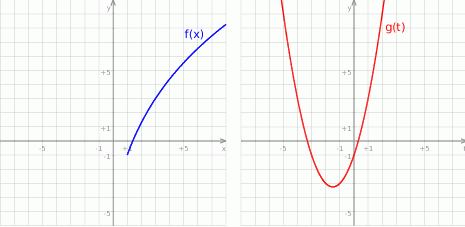
Aby wyznaczyć zbiór wartości zapiszmy wzór funkcji w postaci
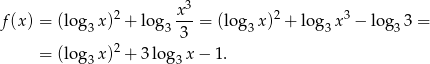
Jeżeli podstawimy teraz 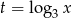 otrzymamy funkcję kwadratową
otrzymamy funkcję kwadratową
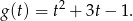
Zwróćmy koniecznie uwagę na to, że ze względu na założenie 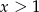 mamy
mamy 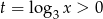 . Zatem wyznaczamy wartości funkcji
. Zatem wyznaczamy wartości funkcji 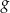 tylko dla
tylko dla 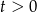 . Wykresem funkcji
. Wykresem funkcji 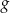 jest parabola o ramionach skierowanych w górę i wierzchołku na lewo od osi
jest parabola o ramionach skierowanych w górę i wierzchołku na lewo od osi 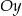 (bo
(bo 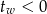 ), więc dla
), więc dla 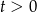 funkcja jest rosnąca i jej zbiór wartości jest równy
funkcja jest rosnąca i jej zbiór wartości jest równy
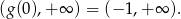
Dokładnie taki sam jest zbiór wartości funkcji 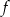 .
.
Odpowiedź: