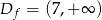Zadanie nr 3342547
Wyznacz dziedzinę funkcji 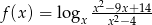 .
.
Rozwiązanie
Ze względu na  w podstawie logarytmu, musimy mieć
w podstawie logarytmu, musimy mieć 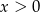 i
i 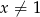 . Ze względu na mianownik ułamka, musi być ponadto
. Ze względu na mianownik ułamka, musi być ponadto 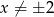 . Ostatni warunek, to dodatniość wyrażenia pod logarytmem. Zacznijmy od znalezienia pierwiastków licznika
. Ostatni warunek, to dodatniość wyrażenia pod logarytmem. Zacznijmy od znalezienia pierwiastków licznika
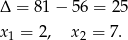
Możemy więc wyrażenie pod logarytmem zapisać w postaci
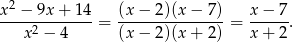
Zauważmy teraz, że mianownik jest dodatni (bo 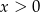 ), więc pozostaje nam warunek
), więc pozostaje nam warunek 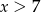 . Tak się miło składa, że jest on silniejszy od wszystkich poprzednich.
. Tak się miło składa, że jest on silniejszy od wszystkich poprzednich.
Odpowiedź: