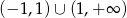/Szkoła średnia/Funkcje/Logarytm

Zadanie nr 3915311

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji 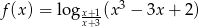3 f(x ) = lo gxx++13(x − 3x + 2) .

Rozwiązanie

Podstawa logarytmu musi być dodatnia i różna od 1. Mamy więc

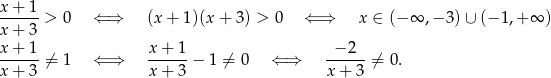
x + 1 ------> 0 ⇐ ⇒ (x + 1)(x + 3) > 0 ⇐ ⇒ x ∈ (− ∞ ,− 3) ∪ (−1 ,+∞ ) x + 3 x-+-1-⁄= 1 ⇐ ⇒ x-+-1-− 1 ⁄= 0 ⇐ ⇒ -−-2--⁄= 0. x + 3 x + 3 x+ 3

Dodatkowo, wyrażenie które logarytmujemy musi być dodatnie. Aby ustalić, kiedy tak jest, rozkładamy wielomian

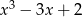
3 x − 3x + 2

na czynniki. Szukamy pierwiastków wielomianu wśród dzielników wyrazu wolnego. Łatwo zauważyć, że jednym z pierwiastków jest 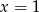x = 1 . Dzielimy więc wielomian przez 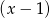(x − 1) – my zrobimy to grupując wyrazy.

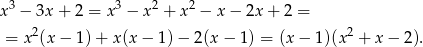
x3 − 3x + 2 = x3 − x2 + x2 − x− 2x+ 2 = 2 2 = x (x − 1 )+ x (x− 1)− 2(x− 1) = (x − 1)(x + x − 2).

Rozkładamy teraz trójmian w drugim nawiasie.

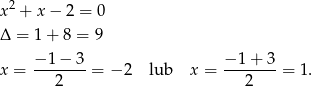
2 x + x− 2 = 0 Δ = 1 + 8 = 9 − 1 − 3 − 1 + 3 x = ------- = − 2 lub x = ------- = 1. 2 2

Zatem

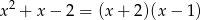
2 x + x − 2 = (x + 2)(x− 1)

i

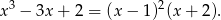
3 2 x − 3x + 2 = (x − 1) (x + 2 ).

Wyrażenie to jest dodatnie, gdy 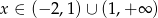x ∈ (− 2,1)∪ (1,+ ∞ ) . W połączeniu z wcześniej otrzymanymi nierównościami oznacza to, że dziedziną funkcji 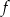f jest zbiór

(− 1,1)∪ (1 ,+∞ ).

 
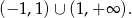
Odpowiedź: (− 1,1) ∪ (1,+ ∞ )

Wersja PDF