/Szkoła średnia/Funkcje/Logarytm

Zadanie nr 5651531

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji 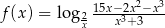15x−2x2−x3 f(x ) = lo g2x x3+ 3

Rozwiązanie

Podstawa logarytmu musi być dodatnia i różna od 1, więc mamy

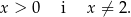
x > 0 i x ⁄= 2.

Przy tym założeniu mianownik ułamka będącego argumentem logarytmu jest dodatni, więc pozostaje do rozwiązania nierówność

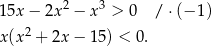
2 3 15x − 2x − x > 0 /⋅ (− 1) x (x2 + 2x− 15) < 0.

Wiemy już, że 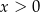x > 0 , więc pozostaje nierówność

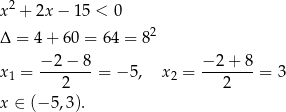
x 2 + 2x − 1 5 < 0 Δ = 4 + 60 = 6 4 = 82 − 2− 8 − 2 + 8 x1 = ------- = − 5, x2 = ------- = 3 2 2 x ∈ (− 5,3 ).

W połączeniu z warunkiem otrzymanym na samym początku zadania, mamy więc

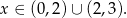
x ∈ (0,2 )∪ (2,3).

 
Odpowiedź: x ∈ (0,2) ∪ (2,3)

Wersja PDF