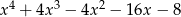Zadanie nr 1958064
Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba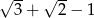 
.
Rozwiązanie
Pomysł jest następujący: oznaczymy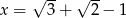 
i będziemy podnosić do kwadratu tak, aby pozbyć się pierwiastków.
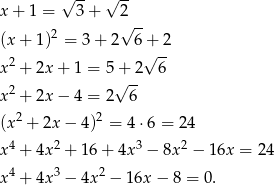
Dla ciekawskich, liczby dla których da się wykonać tego typu sztuczkę, tzn. liczby, które są pierwiatkami wielomianów o współczynnikach całkowitych nazywają się liczbami algebraicznymi. Oczywiście liczby wymierne są algebraiczne, algebraiczne są też pierwiastki z liczb wymiernych (pierwiastki wielomianu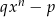 
). Okazuje się również, że zbiór liczb algebraicznych jest zamknięty ze względu na dodawanie, odejmowanie, mnożenie i dzielenie (o ile nie dzielimy przez 0). W szczególności algebraiczne są wszystkie wyrażenia w których są sumy, różnice, iloczyny i ilorazy pierwiatków z liczb wymiernych. Okazuje się, że są też liczby, które nie są algebraiczne, przykładami takich liczb są 
, 
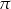(podstawa logarytmu naturalnego) lub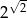 
.
Odpowiedź: 
