Zadanie nr 1980227
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 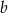 i
i  , funkcja
, funkcja
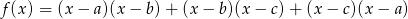
ma co najmniej jedno miejsce zerowe.
Rozwiązanie
Sposób I
Przekształćmy dany wzór funkcji tak, aby obliczyć 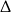 -ę.
-ę.
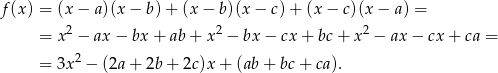
Liczymy 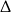 -ę.
-ę.
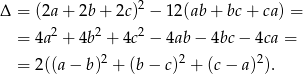
Ponieważ 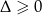 , równanie ma zawsze co najmniej jeden pierwiastek rzeczywisty.
, równanie ma zawsze co najmniej jeden pierwiastek rzeczywisty.
Sposób II
Aby wykazać, że funkcja ma co najmniej jedno miejsce zerowe wystarczy pokazać, że przyjmuje ona zarówno wartość dodatnią jak i ujemną (tak naprawdę, do uzasadnienia tego potrzebna jest ciągłość funkcji wielomianowej, ale ponieważ ciągłość wyleciała z programu szkolnego, więc nie będziemy się nad tym rozwodzić).
Jeżeli założymy, że 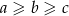 (gdyby kolejność była inna to możemy zmienić nazwy literek) to
(gdyby kolejność była inna to możemy zmienić nazwy literek) to
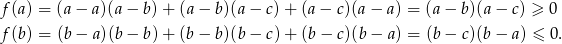
Widać więc, że funkcja musi przecinać oś  .
.

