Zadanie nr 2088835
Wykaż, że wielomian 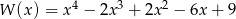 nie ma pierwiastków rzeczywistych.
nie ma pierwiastków rzeczywistych.
Rozwiązanie
Zadanie jest trochę podchwytliwe – ma złapać uczniów stosujących schematy, więc najpierw pokażemy jak nie należy go rozwiązywać, jeżeli kogoś to nie interesuje, to może opuścić następny akapit.
Pierwszą rzeczą, którą każdy robi w takim zadaniu to sprawdza czy wielomian ten ma pierwiastki wymierne, tzn. sprawdzamy czy nie jest równy zero dla liczb postaci 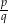 , gdzie
, gdzie 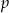 dzielnik wyrazu wolnego (w tym przypadku 9) a
dzielnik wyrazu wolnego (w tym przypadku 9) a 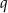 dzielnik współczynnika przy najwyższej potędze (tu 1). Jak się sprawdzi wszystkie możliwości (czyli
dzielnik współczynnika przy najwyższej potędze (tu 1). Jak się sprawdzi wszystkie możliwości (czyli 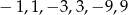 ), to okazuje się, że dla żadnej z tych liczb wielomian się nie zeruje – w kontekście treści zadania nie powinno to dziwić, przecież mamy wykazać, że on się nigdy nie zeruje. W tym miejscu wiele osób może się nabrać – czy już udowodniliśmy, że ten wielomian się nie zeruje? Nie, wykazaliśmy jedynie, że nie ma on pierwiastków wymiernych i tą metodą nic więcej nie uda nam się udowodnić. Żeby jeszcze wyraźniej podkreślić dlaczego ten sposób rozwiązania do niczego nie prowadzi, rozważmy wielomian
), to okazuje się, że dla żadnej z tych liczb wielomian się nie zeruje – w kontekście treści zadania nie powinno to dziwić, przecież mamy wykazać, że on się nigdy nie zeruje. W tym miejscu wiele osób może się nabrać – czy już udowodniliśmy, że ten wielomian się nie zeruje? Nie, wykazaliśmy jedynie, że nie ma on pierwiastków wymiernych i tą metodą nic więcej nie uda nam się udowodnić. Żeby jeszcze wyraźniej podkreślić dlaczego ten sposób rozwiązania do niczego nie prowadzi, rozważmy wielomian  . Ten wielomian też nie ma pierwiastków wymiernych, ale nie jest prawdą, że nie ma pierwiastków.
. Ten wielomian też nie ma pierwiastków wymiernych, ale nie jest prawdą, że nie ma pierwiastków.
Po tym przydługim wywodzie, możemy w końcu wziąć się za rozwiązanie. Jeżeli chcemy wykazać, że wielomian 4 stopnia nie ma pierwiatków, to musimy wykazać, że jest on zawsze dodatni (bo dla 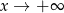 jego wartości są dodatnie, więc jeżeli ma nie mieć pierwiastków, to musi być cały czas ponad osią). Musimy więc wykazać, że
jego wartości są dodatnie, więc jeżeli ma nie mieć pierwiastków, to musi być cały czas ponad osią). Musimy więc wykazać, że
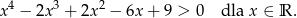
Sposób I
Typowym trickiem na wykazanie czegoś takiego jest zapisanie lewej strony jako sumy kwadratów:
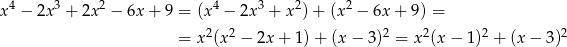
Pozstaje teraz zauważyć, że otrzymane wyrażenie zawsze jest dodatnie – to jest jasne pierwszy składnik zeruje się dla 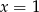 lub
lub 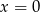 a drugi dla
a drugi dla 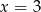 .
.
Jak wpaść na powyższy rozkład? Najłatwiej zacząć od prawej części 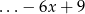 , żeby zrobić z tego kwadrat brakuje
, żeby zrobić z tego kwadrat brakuje 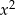 , trzeba go więc dopisać. Dalej rozkład "robi się sam".
, trzeba go więc dopisać. Dalej rozkład "robi się sam".
Sposób II
Jeżeli ktoś jakimś cudem oparł się zreformowanej edukacji i wie co to są pochodne, to mógł to zadanie zrobić „na chama". Wystarczy pokazać, że minima danego wielomianu są powyżej osi – wtedy cały wielomian jest powyżej osi (bo jest stopnia 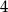 i ma dodatni współczynnik przy
i ma dodatni współczynnik przy 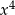 ).
).
Aby to wykazać, liczymy pochodną
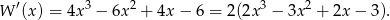
Szukamy teraz pierwiastków wielomianu w nawiasie – jeden z nich to 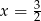 i rozkładamy z twierdzenia Bézout. Możemy też rozłożyć wprost:
i rozkładamy z twierdzenia Bézout. Możemy też rozłożyć wprost:
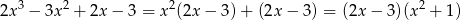
Teraz widać, że pochodna ma jedno miesce zerowe i zmienia w nim znak z „-" na „+", co oznacza, że wyjściowa funkcja ma w tym punkcie minimum. Pozostaje teraz sprawdzić, że
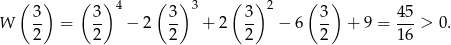
Jak już wcześniej zauważyliśmy, powyższa nierówność oznacza, że 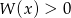 dla każdego
dla każdego 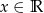 . Dla ciekawych dołączamy wykres danego wielomianu.
. Dla ciekawych dołączamy wykres danego wielomianu.