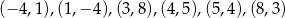/Konkursy/Zadania/Równania

Zadanie nr 2981527

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie pary 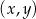(x,y) , gdzie x i y są liczbami całkowitymi spełniającymi równanie

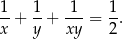
1-+ 1-+ 1--= 1. x y xy 2

Rozwiązanie

Przekształcamy dane równanie

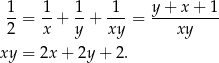
1 1 1 1 y+ x+ 1 --= --+ --+ ---= ---------- 2 x y xy xy xy = 2x + 2y+ 2.

Sposób I

Próbujemy przekształcić dane równanie, tak aby otrzymać z jednej strony iloczyn.

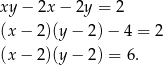
xy − 2x − 2y = 2 (x− 2)(y− 2)− 4 = 2 (x− 2)(y− 2) = 6.

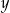Ponieważ x i y są liczbami całkowitymi mamy stąd 8 możliwości

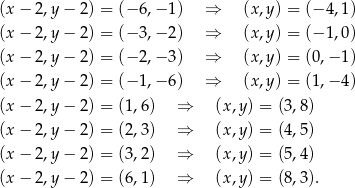
(x − 2 ,y − 2 ) = (− 6,− 1) ⇒ (x,y) = (− 4 ,1 ) (x − 2 ,y − 2 ) = (− 3,− 2) ⇒ (x,y) = (− 1 ,0 ) (x − 2 ,y − 2 ) = (− 2,− 3) ⇒ (x,y) = (0 ,−1 ) (x − 2 ,y − 2 ) = (− 1,− 6) ⇒ (x,y) = (1 ,−4 ) (x − 2 ,y − 2 ) = (1,6) ⇒ (x,y ) = (3,8) (x − 2 ,y − 2 ) = (2,3) ⇒ (x,y ) = (4,5) (x − 2 ,y − 2 ) = (3,2) ⇒ (x,y ) = (5,4) (x − 2 ,y − 2 ) = (6,1) ⇒ (x,y ) = (8,3).

Rozwiązania z zerem musimy oczywiście odrzucić.

Sposób II

Tym razem przekształcamy równanie tak, aby wyznaczyć jedną niewiadomą w zależności od drugiej.

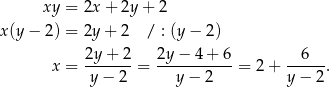
xy = 2x + 2y + 2 x (y − 2 ) = 2y + 2 / : (y− 2) 2y-+-2- 2y-−-4-+-6- --6--- x = y− 2 = y − 2 = 2+ y− 2.

Po drodze dzieliliśmy przez 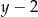y − 2 – mogliśmy tak zrobić, bo łatwo sprawdzić, że dla 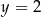y = 2 równanie jest sprzeczne. Powyższa równość oznacza, że 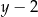y − 2 musi być dzielnikiem 6, czyli

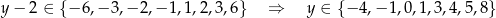
y− 2 ∈ {− 6,− 3,− 2,− 1,1,2,3,6 } ⇒ y ∈ {− 4,− 1,0,1 ,3 ,4,5,8}

Wtedy odpowiednio

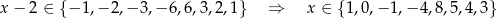
x− 2 ∈ {− 1,− 2,− 3,− 6,6,3,2,1 } ⇒ x ∈ {1,0 ,−1 ,−4 ,8,5,4,3}

Rozwiązania z zerem odrzucamy i otrzymujemy dokładnie te same rozwiązania, co w poprzednim sposobie.  
Odpowiedź: (− 4,1),(1,− 4),(3,8),(4,5 ),(5 ,4),(8,3)

Wersja PDF