Zadanie nr 4740509
Wykaż, że nie istnieje para liczb 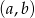 spełniająca układ równań
spełniająca układ równań 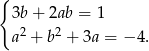
Rozwiązanie
Sposób I
Dodajmy równania układu stronami.
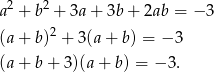
Podstawmy teraz 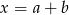 .
.
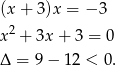
Otrzymane równanie kwadratowe jest sprzeczne, więc układ nie ma rozwiązań.
Sposób II
Przekształćmy drugie równanie – zwijamy do pełnego kwadratu.
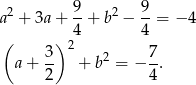
Oczywiście suma kwadratów nie może być liczbą ujemną, więc drugie równanie układu jest sprzeczne.
Sposób III
Podstawiamy 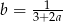 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
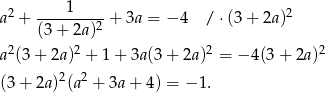
Teraz wystarczy zauważyć, że oba wyrażenia z lewej strony są nieujemne (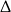 trójmianu w drugim nawiasie jest ujemna). Równanie to jest więc sprzeczne.
trójmianu w drugim nawiasie jest ujemna). Równanie to jest więc sprzeczne.

