Zadanie nr 6261209
Ile jest takich czwórek liczb całkowitych i dodatnich 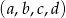 , które spełniają równanie
, które spełniają równanie 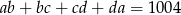 .
.
Rozwiązanie
Podane równanie możemy zapisać w postaci
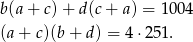
Liczba 251 jest liczbą pierwszą, więc 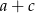 może być równe 2,4,251,502. Żeby trochę sobie te rachunki uprościć załóżmy, że
może być równe 2,4,251,502. Żeby trochę sobie te rachunki uprościć załóżmy, że 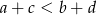 i na koniec pomnożymy otrzymaną liczbę możliwości przez 2.
i na koniec pomnożymy otrzymaną liczbę możliwości przez 2.
Zatem 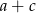 może być równe 2 lub 4.
może być równe 2 lub 4.
Jeżeli 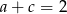 to
to 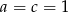 i
i 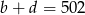 . Liczbę
. Liczbę 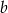 możemy wybrać na 501 sposobów (między 1 a 501), a liczba
możemy wybrać na 501 sposobów (między 1 a 501), a liczba 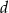 jest już wyznaczona jednoznacznie. Mamy zatem w tym przypadku 501 możliwości.
jest już wyznaczona jednoznacznie. Mamy zatem w tym przypadku 501 możliwości.
Jeżeli 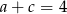 , to parę
, to parę 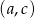 można wybrać na 3 sposoby (
można wybrać na 3 sposoby (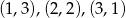 ), a parę
), a parę 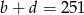 na 250 sposobów. Razem mamy więc w tym przypadku
na 250 sposobów. Razem mamy więc w tym przypadku 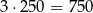 sposobów.
sposobów.
W sumie jest więc
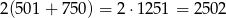
możliwości.
Odpowiedź: 2502 czwórek

