/Konkursy/Zadania/Równania

Zadanie nr 6296453

Uzasadnij, że równanie 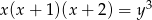3 x (x+ 1)(x + 2) = y nie ma rozwiązań w liczbach całkowitych dodatnich x,y .

Wersja PDF

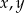Rozwiązanie

Sposób I

Zauważmy, że jeżeli 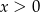x > 0 , to

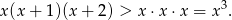
3 x(x + 1 )(x+ 2) > x ⋅x⋅ x = x .

Z drugiej strony

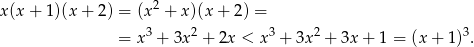
2 x(x+ 1)(x + 2) = (x + x )(x+ 2) = = x 3 + 3x 2 + 2x < x3 + 3x2 + 3x + 1 = (x+ 1)3.

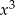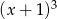To oznacza, że lewa strona równania jest wewnątrz przedziału o końcach x3 i (x + 1)3 , a przedział ten nie zawiera sześcianów liczb całkowitych. Dane równanie jest więc sprzeczne.

Sposób II

Zauważmy, że na mocy nierówności między średnią arytmetyczną i geometryczną mamy

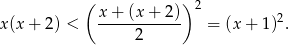
( ) 2 x(x + 2 ) < x+--(x+--2)- = (x + 1)2. 2

Stąd

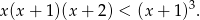
3 x(x + 1)(x+ 2) < (x + 1) .

Dalszą część rozwiązania przeprowadzamy tak samo jak w pierwszym sposobie.

Sposób III

Tak jak w pierwszym sposobie zauważamy, że

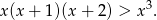
3 x(x + 1 )(x+ 2) > x .

Ponadto

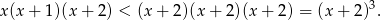
x(x + 1)(x + 2 ) < (x+ 2)(x + 2)(x + 2) = (x + 2 )3.

Jedyny sześcian liczby całkowitej, który spełnia te dwie nierówności, to 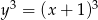y3 = (x+ 1)3 . Mamy zatem

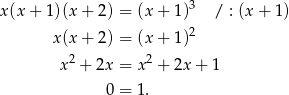
3 x(x + 1 )(x+ 2) = (x + 1) / : (x+ 1) x (x+ 2) = (x + 1)2 2 2 x + 2x = x + 2x + 1 0 = 1.

Dane równanie jest więc sprzeczne.

Wersja PDF