Zadanie nr 7186929
Udowodnij, że jeżeli 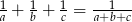 to
to 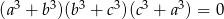 .
.
Rozwiązanie
Sposób I
Przekształćmy podaną równość
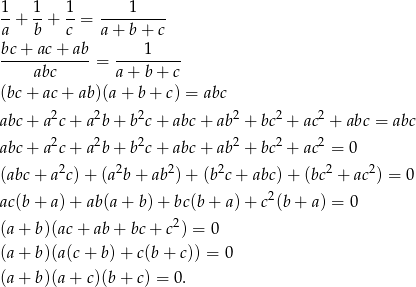
Z powyższej równości wynika, że 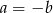 lub
lub 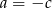 lub
lub 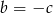 . W każdej z tych sytuacji dostajemy żądaną równość.
. W każdej z tych sytuacji dostajemy żądaną równość.
Sposób II
Zadanie jest łatwe jeżeli skorzystamy ze wzorów Viète’a dla równania stopnia 3:
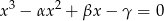
Jeżeli liczby 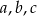 są pierwiastkami tego równania to
są pierwiastkami tego równania to
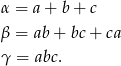
Jak poprzednio dochodzimy do równości
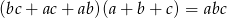
Czyli w naszych nowych znaczkach 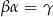 i nasze równanie przybiera postać:
i nasze równanie przybiera postać:
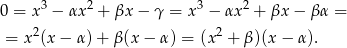
Gołym okiem widać pierwiastek  . Z drugiej strony, wszystkie pierwiastki to
. Z drugiej strony, wszystkie pierwiastki to 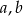 i
i  , więc
, więc  musi być równe jednej z tych liczb. To natychmiast daje
musi być równe jednej z tych liczb. To natychmiast daje 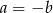 lub
lub 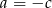 lub
lub 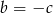 .
.

