/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 2329228

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 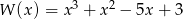3 2 W (x) = x + x − 5x + 3 .

  • Oblicz resztę z dzielenia tego wielomianu przez dwumian (x + 1) .
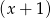  • Oblicz miejsca zerowe tego wielomianu.
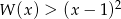  • Rozwiąż nierówność W (x) > (x − 1)2 .

Rozwiązanie

  • Reszta z dzielenia wielomianu 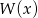W (x) przez dwumian 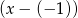(x − (− 1)) to dokładnie 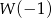W (− 1) . Liczymy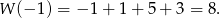
    W (− 1) = − 1+ 1+ 5+ 3 = 8.

     
    Odpowiedź: 8

  • Szukamy najpierw pierwiastków całkowitych, czyli sprawdzamy dzielniki 3, tj. liczby 1,-1,3,-3. Trafiamy od razu, 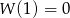W (1) = 0 . Jak już mamy pierwiastek, to dzielimy wielomian przez 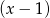(x − 1) . Robimy to tak jak umiemy, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą.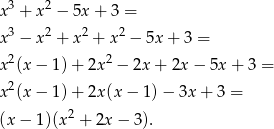
    3 2 x + x − 5x + 3 = x3 − x2 + x2 + x2 − 5x + 3 = 2 2 x (x − 1) + 2x − 2x + 2x − 5x + 3 = x2(x − 1) + 2x(x − 1 )− 3x + 3 = (x− 1)(x2 + 2x − 3).

    Pozostało rozwiązać równanie kwadratowe, 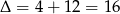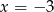Δ = 4 + 12 = 16 , x = − 3 lub x = 1 .  
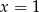    Odpowiedź: -3,1

  • Z poprzedniego podpunktu wiemy, że 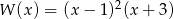W (x) = (x− 1)2(x+ 3) . Mamy zatem nierówność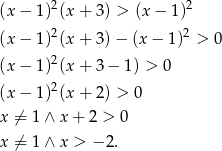
    (x − 1)2(x + 3 ) > (x− 1)2 2 2 (x − 1) (x + 3 )− (x − 1 ) > 0 (x − 1)2(x + 3 − 1 ) > 0 2 (x − 1) (x + 2 ) > 0 x ⁄= 1∧ x + 2 > 0 x ⁄= 1∧ x > − 2.

     
    Odpowiedź: x ∈ (− 2,1)∪ (1,∞ )

Wersja PDF