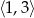Zadanie nr 2355956
Wyznacz przedziały monotoniczności funkcji 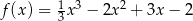 .
.
Rozwiązanie
Aby znaleźć przedziały monotoniczności liczymy pochodną i szukamy jej miejsc zerowych.
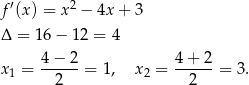
Ponieważ pochodna jest dodatnia na przedziałach 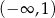 i
i 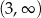 oraz ujemna na
oraz ujemna na 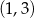 , funkcja
, funkcja 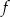 jest na tych zbiorach odpowiednio rosnąca i malejąca. Aby otrzymać maksymalne przedziały monotoniczności dodajemy też końce przedziałów.
jest na tych zbiorach odpowiednio rosnąca i malejąca. Aby otrzymać maksymalne przedziały monotoniczności dodajemy też końce przedziałów.
Na koniec, dla ciekawskich, wykres funkcji 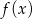 .
.
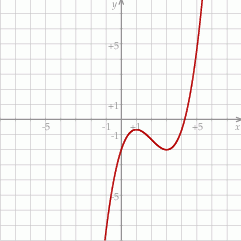
Odpowiedź: Rosnąca na 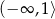 i
i 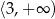 , malejąca na
, malejąca na