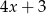/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 2373887

Dodaj do ulubionych
Dodaj do rozwiązanych

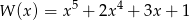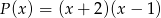Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu W (x) = x5 + 2x4 + 3x + 1 przez P (x) = (x + 2)(x − 1 ) .

Rozwiązanie

Reszta 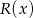R (x) z dzielenia przez wielomian 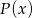P(x ) jest wielomianem stopnia 1 takim, że

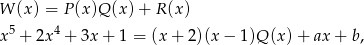
W (x) = P(x)Q (x) + R (x) x5 + 2x4 + 3x + 1 = (x+ 2)(x− 1)Q (x)+ ax + b,

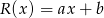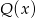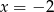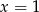gdzie R (x) = ax + b i Q (x) jest pewnym wielomianem. Podstawmy w tej równości x = − 2 i x = 1 (miejsca zerowe P(x) ).

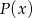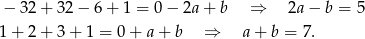
− 32 + 32 − 6 + 1 = 0 − 2a + b ⇒ 2a − b = 5 1 + 2 + 3+ 1 = 0 + a + b ⇒ a + b = 7 .

Dodając te dwa równania stronami (żeby skrócić 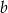b ) mamy

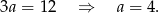
3a = 1 2 ⇒ a = 4.

Stąd 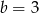b = 3 .  
Odpowiedź: 4x + 3

Wersja PDF