/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 2620698

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 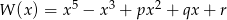5 3 2 W (x) = x − x + px + qx + r jest podzielny przez wielomian 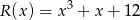R (x) = x 3 + x + 12 . Wyznacz liczby 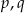p ,q i r .

Rozwiązanie

Sposób I

Można na początku spróbować rozłożyć wielomian 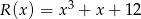3 R (x) = x + x + 12 na czynniki, ale nic z tego nie wyjdzie – wielomian ten nie ma pierwiastków wymiernych.

Spróbujmy więc inaczej, skoro 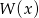W (x) dzieli się przez 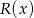R(x) to dla pewnego wielomianu 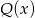Q (x) mamy

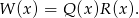
W (x) = Q (x)R (x).

W dodatku trochę wiemy o 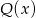Q (x) - musi mieć stopień 2 i musi mieć współczynnik 1 przy 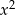x2 . Szukamy więc wielomianu 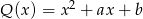Q (x) = x2 + ax+ b spełniającego równość

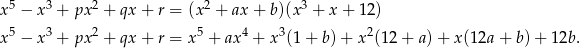
x5 − x3 + px2 + qx + r = (x 2 + ax + b)(x3 + x+ 12) 5 3 2 5 4 3 2 x − x + px + qx + r = x + ax + x (1+ b)+ x (12 + a)+ x(12a + b) + 12b .

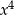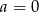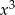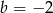Dwa wielomiany są równe jeżeli mają równe współczynniki, więc patrząc na współczynnik przy x4 otrzymujemy a = 0 , a patrząc na współczynnik przy 3 x mamy b = − 2 . Porównując pozostałe współczynniki dostajemy

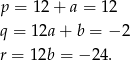
p = 12+ a = 12 q = 12a + b = − 2 r = 12b = − 24.

Sposób II

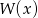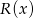Dzielimy W (x) przez R (x) ignorując parametry – my zrobimy to grupując wyrazy.

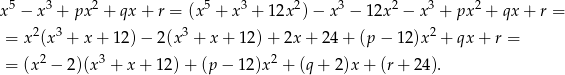
x5 − x3 + px2 + qx + r = (x 5 + x 3 + 1 2x2)− x3 − 12x2 − x3 + px 2 + qx + r = = x2(x3 + x + 12 )− 2(x 3 + x + 12)+ 2x+ 24 + (p − 12)x 2 + qx + r = 2 3 2 = (x − 2)(x + x + 12) + (p − 12 )x + (q+ 2)x+ (r+ 2 4).

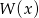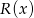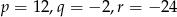Skoro wielomian W (x) ma się dzielić przez R (x) bez reszty, otrzymana reszta musi być równa 0. Zatem p = 12,q = − 2,r = − 24 .  
Odpowiedź: (p ,q ,r) = (12,− 2,− 24)

Wersja PDF