/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 3039652

Dodaj do ulubionych
Dodaj do rozwiązanych

Reszta z dzielenia wielomianu 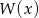W (x) przez wielomian 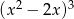2 3 (x − 2x ) jest równa 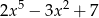2x 5 − 3x 2 + 7 . Oblicz resztę z dzielenia wielomianu 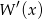W ′(x) przez dwumian (x − 2) .

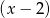Rozwiązanie

Sposób I

Wiemy, że

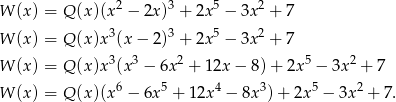
W (x) = Q (x )(x2 − 2x)3 + 2x5 − 3x2 + 7 3 3 5 2 W (x) = Q (x )x (x− 2) + 2x − 3x + 7 3 3 2 5 2 W (x) = Q (x )x (x − 6x + 12x − 8) + 2x − 3x + 7 W (x) = Q (x )(x6 − 6x5 + 12x4 − 8x3) + 2x 5 − 3x 2 + 7 .

dla pewnego wielomianu 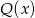Q (x) . Liczymy pochodną z obu stron (korzystamy ze wzoru na pochodną iloczynu).

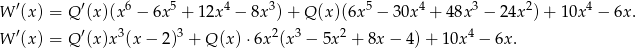
W ′(x) = Q ′(x)(x6 − 6x5 + 12x 4 − 8x 3)+ Q (x )(6x 5 − 30x4 + 48x3 − 24x 2)+ 10x4 − 6x. W ′(x) = Q ′(x)x3(x − 2)3 + Q (x)⋅ 6x2(x3 − 5x2 + 8x − 4 )+ 10x 4 − 6x.

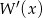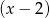Reszta z dzielenia ′ W (x ) przez (x− 2) , to po prostu 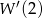′ W (2) . Liczymy

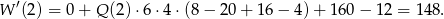
′ W (2 ) = 0+ Q (2 )⋅6 ⋅4 ⋅(8− 20+ 16− 4)+ 160 − 12 = 1 48.

Sposób II

Tak jak poprzednio zauważmy, że

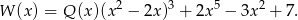
W (x) = Q (x)(x 2 − 2x )3 + 2x 5 − 3x2 + 7.

Tym razem jednak obliczamy pochodną ze wzoru na pochodną funkcji złożonej.

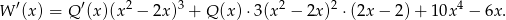
W ′(x) = Q′(x)(x 2 − 2x )3 + Q (x )⋅3(x 2 − 2x )2 ⋅(2x − 2 )+ 10x 4 − 6x.

Interesująca nas reszta jest więc równa

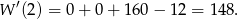
W ′(2 ) = 0+ 0+ 160 − 12 = 14 8.

 
Odpowiedź: 148

Wersja PDF