/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 3743729

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 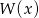W (x) stopnia 3 jest podzielny przez trójmian kwadratowy 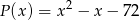P (x) = x2 − x − 72 . Wiadomo ponadto, że 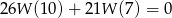26W (10) + 21W (7) = 0 . Wyznacz miejsca zerowe wielomianu W (x) .

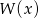Rozwiązanie

Rozłóżmy najpierw wielomian 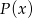P(x ) .

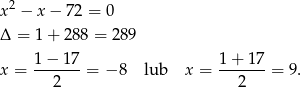
2 x − x − 7 2 = 0 Δ = 1 + 288 = 289 1 − 17 1 + 17 x = -------= − 8 lub x = -------= 9. 2 2

To oznacza, że

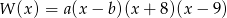
W (x) = a(x − b)(x + 8)(x − 9 )

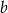dla pewnych a i b . Pozostało teraz zapisać podaną informację o wartościach W (x) .

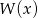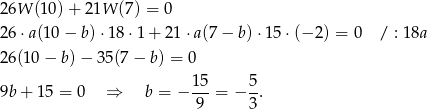
26W (10 )+ 21W (7) = 0 26⋅ a(10− b)⋅1 8⋅1 + 21 ⋅a(7 − b) ⋅15 ⋅(− 2) = 0 / : 18a 26(10 − b) − 35(7 − b) = 0 15- 5- 9b+ 15 = 0 ⇒ b = − 9 = − 3.

 
Odpowiedź: { } − 8,9,− 53

Wersja PDF