/Szkoła średnia/Funkcje/Wielomiany

Zadanie nr 3886482

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 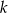k reszta z dzielenia wielomianu 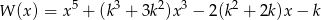W (x) = x5 + (k3 + 3k2)x3 − 2(k2 + 2k)x − k przez dwumian 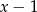x− 1 jest nie większa od (–2)?

Rozwiązanie

Reszta z dzielenia wielomianu 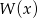W (x) przez dwumian 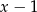x − 1 to po prostu wartość 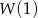W (1 ) . Rzeczywiście, jeżeli

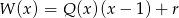
W (x) = Q (x)(x − 1 )+ r

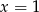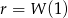to wstawiając w tej równości x = 1 mamy r = W (1) . Musimy więc rozwiązać nierówność.

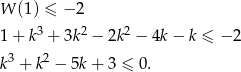
W (1) ≤ − 2 3 2 2 1 + k + 3k − 2k − 4k − k ≤ − 2 k 3 + k2 − 5k + 3 ≤ 0 .

Szukamy pierwiastka lewej strony. Sprawdzając dzielniki wyrazu wolnego łatwo znaleźć pierwiastek 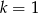k = 1 . Dzielimy lewą stronę przez 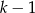k − 1 . My zrobimy to grupując wyrazy.

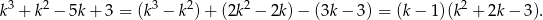
k3+ k2− 5k + 3 = (k3− k2) + (2k2− 2k)− (3k− 3) = (k− 1)(k2+ 2k − 3 ).

Teraz rozkładamy trójmian w nawiasie.

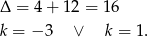
Δ = 4+ 1 2 = 16 k = − 3 ∨ k = 1 .

Mamy zatem nierówność

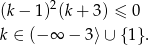
(k− 1)2(k+ 3 ) ≤ 0 k ∈ (− ∞ − 3 ⟩∪ {1} .

 
Odpowiedź: k ∈ (− ∞ − 3⟩ ∪ {1}

Wersja PDF