/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Różne

Zadanie nr 2168404

Dodaj do ulubionych
Dodaj do rozwiązanych

W okrąg o równaniu 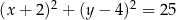2 2 (x+ 2) + (y− 4) = 25 wpisano trójkąt 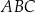ABC , którego pole jest równe 20. Bok 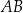AB tego trójkąta jest zawarty w prostej o równaniu 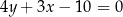4y + 3x − 10 = 0 , a wysokość opuszczona z wierzchołka 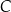C przecina bok 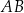AB w punkcie 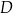D , którego obie współrzędne są dodatnie. Oblicz współrzędne punktu D .

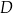Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.