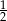/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Różne

Zadanie nr 3548116

Dodaj do ulubionych
Dodaj do rozwiązanych

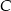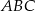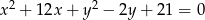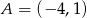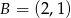Wierzchołek C trójkąta ABC leży na okręgu o równaniu 2 2 x + 12x + y − 2y + 21 = 0 , a pozostałe wierzchołki mają współrzędne A = (− 4,1) i B = (2,1 ) . Oblicz wartość wyrażenia

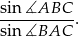
sin-∡ABC---. sin ∡BAC

Rozwiązanie

Zacznijmy od ustalenia jaki jest środek i promień danego okręgu.

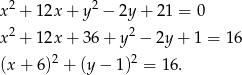
2 2 x + 1 2x+ y − 2y+ 21 = 0 x 2 + 1 2x+ 36+ y2 − 2y + 1 = 16 2 2 (x + 6 ) + (y − 1) = 16.

Jest więc okrąg o środku w punkcie 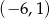(−6 ,1) i promieniu 4.

PIC

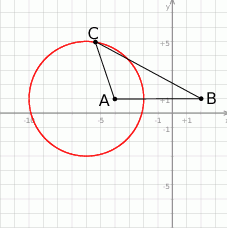
Na mocy twierdzenia sinusów możemy podany stosunek sinusów zamienić na stosunek długości odpowiednich boków.

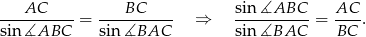
---AC----- = ---BC----- ⇒ sin-∡ABC-- = AC--. sin∡ABC sin ∡BAC sin ∡BAC BC

Pozostało policzyć wartość tego ilorazu. Żeby nie przepisywać pierwiastków będziemy liczyć kwadrat ilorazu. Oznaczmy 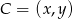C = (x,y) .

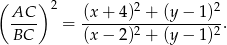
( ) AC 2 (x + 4)2 + (y− 1)2 BC-- = (x-−-2)2 +-(y−--1)2.

Korzystamy teraz z tego, że punkt 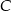C leży na danym okręgu, czyli 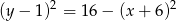2 2 (y − 1) = 1 6− (x+ 6) . Mamy więc

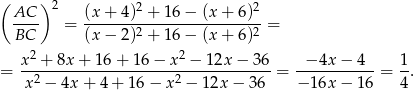
( ) 2 2 2 AC-- = (x-+--4)-+-1-6−-(x-+--6)-= BC (x − 2)2 + 1 6− (x + 6)2 2 2 = x-+--8x-+-16-+-16-−-x--−-12x-−--36-= --−4x-−--4- = 1. x 2 − 4x + 4+ 16− x2 − 12x − 36 − 16x − 16 4

Zatem

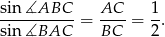
sin ∡ABC AC 1 ---------- = ---- = --. sin ∡BAC BC 2

 
Odpowiedź: 1 2

Wersja PDF