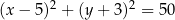Zadanie nr 4158930
W trójkącie  , w którym
, w którym 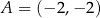 oraz
oraz 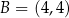 , kąt przy wierzchołku
, kąt przy wierzchołku 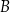 jest rozwarty. Bok
jest rozwarty. Bok 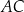 zawiera się w prostej
zawiera się w prostej 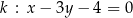 . Środek okręgu opisanego na trójkącie
. Środek okręgu opisanego na trójkącie 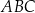 znajduje się w odległości
znajduje się w odległości 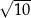 od boku
od boku 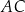 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
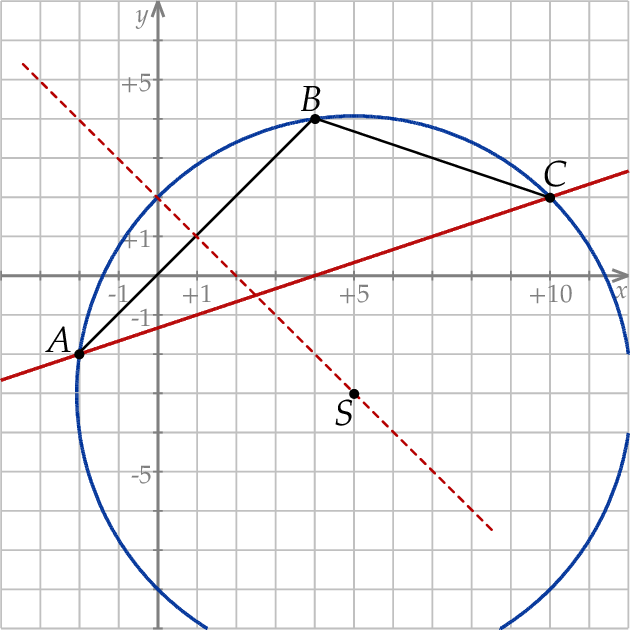
Środek okręgu opisanego na trójkącie to punkt wspólny symetralnych jego boków. W naszej sytuacji łatwo napisać równanie jednej z symetralnych, więc od tego zacznijmy.
Symetralna boku 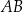 to zbiór punktów
to zbiór punktów 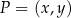 , które są tak samo odległe od
, które są tak samo odległe od 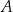 i od
i od 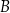 . Mamy stąd równanie
. Mamy stąd równanie
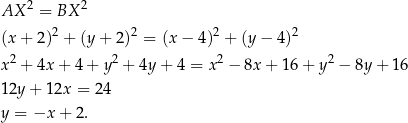
Oczywiście równanie symetralnej odcinka 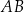 mogliśmy napisać na różne inne sposoby: np. korzystając z tego, że jest to prosta prostopadła do prostej
mogliśmy napisać na różne inne sposoby: np. korzystając z tego, że jest to prosta prostopadła do prostej 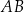 i przechodząca przez środek odcinka
i przechodząca przez środek odcinka 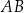 , albo korzystając ze wzoru na prostą prostopadłą do wektora i przechodzącą przez punkt.
, albo korzystając ze wzoru na prostą prostopadłą do wektora i przechodzącą przez punkt.
Zapiszmy teraz informację o odległości środka 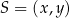 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 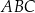 od danej prostej
od danej prostej 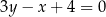 . Korzystając ze wzoru na odległość punktu od prostej mamy
. Korzystając ze wzoru na odległość punktu od prostej mamy
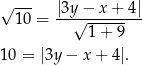
Aby opuścić wartość bezwzględną, zauważmy, że informacja o tym, że kąt 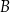 jest rozwarty oznacza, że środek okręgu opisanego na trójkącie
jest rozwarty oznacza, że środek okręgu opisanego na trójkącie 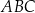 leży na zewnątrz tego trójkąta, czyli w naszej sytuacji poniżej prostej
leży na zewnątrz tego trójkąta, czyli w naszej sytuacji poniżej prostej 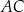 . W takim razie współrzędne punktu
. W takim razie współrzędne punktu 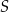 spełniają nierówność
spełniają nierówność 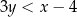 i powyższy warunek przyjmuje postać
i powyższy warunek przyjmuje postać
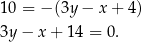
Współrzędne punktu 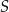 spełniają więc układ równań
spełniają więc układ równań
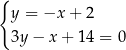
Podstawiamy z pierwszego równania do drugiego.
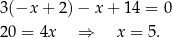
Zatem 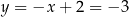 i
i 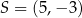 . Musimy jeszcze obliczyć promień
. Musimy jeszcze obliczyć promień 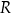 okręgu opisanego.
okręgu opisanego.
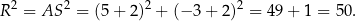
Okrąg opisany ma więc równanie
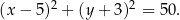
Odpowiedź: