/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Różne

Zadanie nr 4582184

Okrąg wpisany w trójkąt 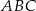ABC ma równanie 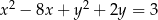2 2 x − 8x + y + 2y = 3 . Oblicz 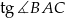tg ∡BAC jeżeli A = (− 4,− 7) .

Wersja PDF

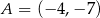Rozwiązanie

Przekształćmy równanie okręgu tak, aby ustalić jaki jest jego środek i promień.

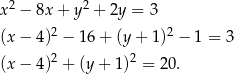
2 2 x − 8x + y + 2y = 3 (x− 4)2 − 16+ (y+ 1)2 − 1 = 3 (x− 4)2 + (y+ 1)2 = 20.

Jest to więc okrąg o środku 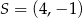S = (4 ,− 1 ) i promieniu 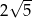√ -- 2 5 . Możemy teraz wykonać szkicowy rysunek.

PIC

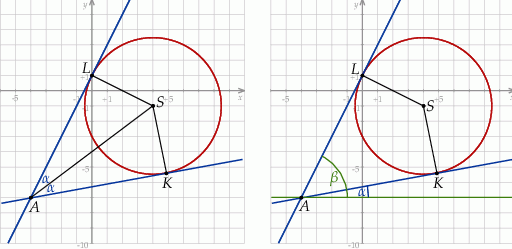
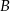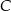Robiąc rysunek trudno nie zauważyć, że z treści zadania nie wynika jakie jest dokładne położenie wierzchołków B i C . Nie ma to jednak żadnego znaczenia, bo kąt 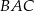BAC jest jednoznacznie wyznaczony przez punkt 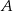A i okrąg wpisany w trójkąt – ramiona tego kąta to styczne do okręgu poprowadzone przez punkt A .

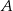Sposób I

Zauważmy, że jeżeli oznaczymy 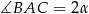∡BAC = 2α to dość łatwo jest obliczyć funkcje trygonometryczne kąta α . Np.

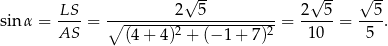
√ -- √ -- √ -- sin α = LS--= ∘--------2---5----------= 2--5-= --5. AS (4 + 4)2 + (− 1 + 7)2 10 5

To z kolei pozwala łatwo obliczyć 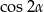cos 2α .

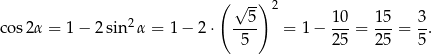
( --) √ 5 2 10 15 3 cos 2α = 1 − 2 sin 2α = 1− 2⋅ ---- = 1− ---= ---= -. 5 25 25 5

Stąd

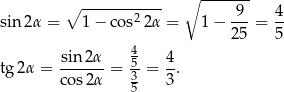
∘ ----------- ∘ ------- sin 2α = 1− cos22α = 1 − -9- = 4- 2 5 5 sin2α 4 4 tg 2α = -------= -53 = --. cos2 α 5 3

Sposób II

Tym razem użyjemy odrobinę więcej geometrii analitycznej i wyznaczymy równania stycznych 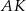AK i AL .

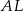Styczne mają przechodzić przez punkt 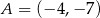A = (− 4,− 7) , więc muszą mieć postać

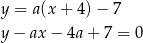
y = a(x+ 4)− 7 y − ax − 4a + 7 = 0

(dla 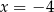x = − 4 musi wychodzić 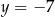y = − 7 ). Tak naprawdę pomijamy w ten sposób pionową prostą przechodzącą przez punkt 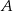A , ale nawet ze szkicowego obrazka widać, że nie jest to szukana styczna.

Prosta jest styczna do okręgu, jeżeli odległość środka okręgu 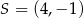S = (4,− 1) od tej prostej jest równa promieniowi okręgu, czyli w naszej sytuacji 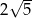√ -- 2 5 . Na mocy wzoru na odległość punktu od prostej mamy więc równanie

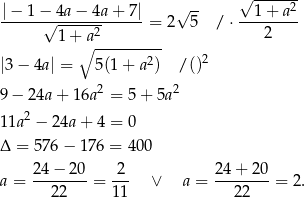
√ -- √ -----2 |−--1−√-4a−--4a+--7|= 2 5 /⋅ --1+--a-- 1+ a2 2 ∘ ---------- 2 |3− 4a| = 5(1 + a2) / () 2 2 9− 24a + 16a = 5+ 5a 11a2 − 24a + 4 = 0 Δ = 576 − 176 = 400 2 4− 2 0 2 24+ 20 a = ---22--- = 1-1 ∨ a = --22----= 2.

Zatem styczne mają równania

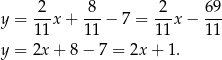
-2- -8- -2- 69- y = 11 x+ 11 − 7 = 11x − 11 y = 2x + 8 − 7 = 2x+ 1.

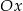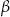Współczynniki kierunkowe stycznych to dokładnie tangensy kątów, jakie tworzą te styczne z osią Ox . Jeżeli oznaczymy te kąty przez α i β (prawy rysunek), to interesujący nas kąt to 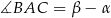∡BAC = β − α . Znajdujemy teraz w tablicach wzór na tangens różnicy i mamy

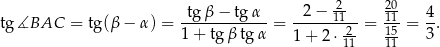
tg β − tgα 2 − 211- 2101 4 tg ∡BAC = tg(β − α) = ------------= -------2- = 15-= --. 1+ tg β tg α 1 + 2 ⋅11 11 3

 
Odpowiedź: 4 3

Wersja PDF