Zadanie nr 7803795
Punkty 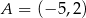 i
i 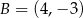 są wierzchołkami trójkąta
są wierzchołkami trójkąta 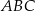 , a wysokości opuszczone z wierzchołków
, a wysokości opuszczone z wierzchołków 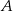 i
i 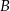 tego trójkąta zawierają się odpowiednio w prostych o równaniach
tego trójkąta zawierają się odpowiednio w prostych o równaniach 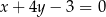 oraz
oraz 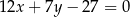 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 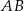 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
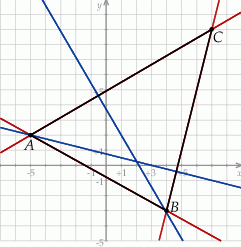
Napiszemy najpierw równanie prostej 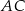 – jest to prosta prostopadła do wysokości
– jest to prosta prostopadła do wysokości 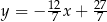 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 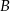 i przechodząca przez punkt
i przechodząca przez punkt 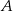 . Jest to więc prosta postaci
. Jest to więc prosta postaci 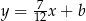 . Współczynnik
. Współczynnik 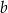 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 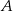 .
.
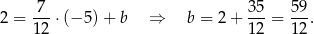
Prosta 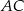 ma więc równanie:
ma więc równanie:
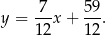
Dokładnie w ten sam sposób wyznaczamy równanie prostej 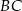 – jest to prosta prostopadła do wysokości
– jest to prosta prostopadła do wysokości 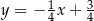 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 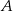 i przechodząca przez punkt
i przechodząca przez punkt 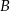 . Jest to więc prosta postaci
. Jest to więc prosta postaci 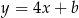 . Współczynnik
. Współczynnik 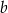 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 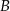 .
.

Prosta 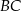 ma więc równanie:
ma więc równanie:
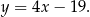
Wyznaczamy teraz punkt wspólny 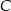 prostych
prostych 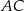 i
i 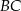 .
.
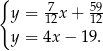
Odejmujemy od drugiego równania pierwsze i mamy
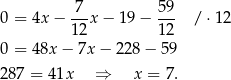
Stąd 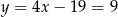 i
i 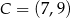 .
.
Interesująca nas długość wysokości opuszczonej na bok 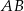 , to dokładnie odległość punktu
, to dokładnie odległość punktu 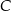 od prostej
od prostej 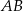 . Napiszmy równanie tej prostej. Szukamy prostej w postaci
. Napiszmy równanie tej prostej. Szukamy prostej w postaci 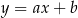 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 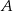 i
i 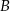 .
.
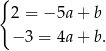
Odejmujemy od drugiego równania pierwsze i mamy
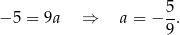
Stąd 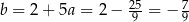 i prosta
i prosta 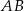 ma równanie
ma równanie
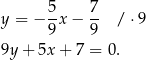
Pozostało obliczyć odległość punktu 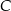 od prostej
od prostej 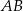 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 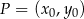 od prostej
od prostej 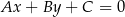 :
:
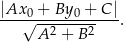
W naszej sytuacji mamy
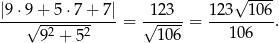
Odpowiedź: