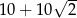Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 8381422

Prosta 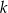k tworzy z dodatnią półosią 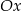Ox kąt o mierze 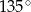∘ 135 i przechodzi przez punkt 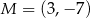M = (3 ,− 7 ) . Prosta 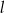l jest prostopadła do prostej 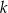k i przecina oś 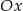Ox w punkcie o odciętej 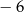− 6 . Oblicz obwód trójkąta utworzonego przez proste 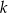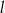k , l i oś Oy .

Wersja PDF
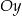Rozwiązanie

Jeżeli prosta 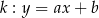k : y = ax+ b przecina oś 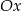Ox pod kątem 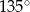∘ 1 35 , to jej współczynnik kierunkowy jest równy

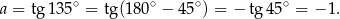
a = tg13 5∘ = tg(180∘ − 45∘) = − tg45 ∘ = − 1.

Wiemy ponadto, że prosta ta przechodzi przez punkt 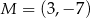M = (3,− 7) , więc

− 7 = − 3+ b ⇒ b = − 4

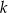i prosta k ma równanie: y = −x − 4 .

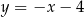Prosta 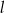l jest prostopadła do 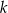k , więc ma równanie postaci 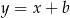y = x + b . Wiemy ponadto, że

0 = −6 + b ⇒ b = 6.

Jest to więc prosta 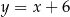y = x + 6 .

PIC

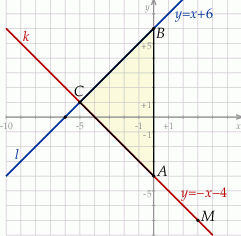
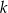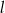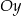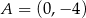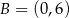Proste k i l przecinają oś Oy odpowiednio w punktach A = (0,− 4) i B = (0,6) . Wyznaczmy jeszcze punkt wspólny 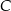C tych prostych.

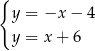
{ y = −x − 4 y = x + 6

Dodajemy równania stronami i mamy

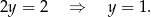
2y = 2 ⇒ y = 1.

Stąd 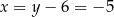x = y − 6 = − 5 i C = (− 5,1 ) .

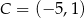Pozostało obliczyć długości boków trójkąta 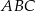ABC .

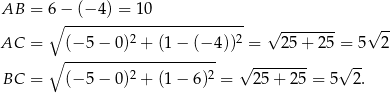
AB = 6− (− 4) = 10 ∘ ------------------------- √ -------- √ -- AC = (− 5 − 0)2 + (1− (− 4))2 = 25 + 25 = 5 2 ∘ --------------------- √ -------- √ -- BC = (− 5 − 0)2 + (1− 6)2 = 25 + 25 = 5 2.

Obwód trójkąta 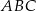ABC jest więc równy

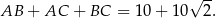
√ -- AB + AC + BC = 10+ 10 2.

 
Odpowiedź: √ -- 10 + 10 2

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!