Zadanie nr 9621371
Boki 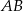 i
i 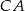 trójkąta
trójkąta 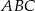 są zawarte w prostych
są zawarte w prostych 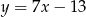 i
i 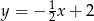 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 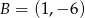 i
i 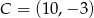 . Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok
. Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok 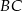 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
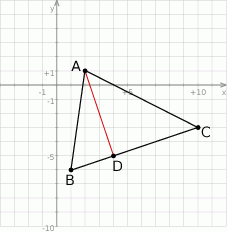
Wyznaczamy najpierw współrzędne wierzchołka 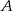 trójkąta – jest to punkt wspólny podanych prostych
trójkąta – jest to punkt wspólny podanych prostych 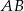 i
i 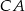 .
.
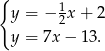
Porównujemy 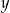 -ki i mamy
-ki i mamy
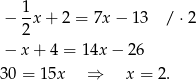
Stąd 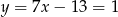 i
i 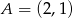 .
.
Wyznaczamy teraz równanie prostej 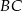 . Szukamy prostej w postaci
. Szukamy prostej w postaci 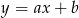 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 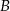 i
i 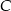 .
.
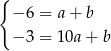
Odejmujemy od drugiego równania pierwsze i mamy 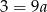 , czyli
, czyli 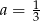 . Stąd
. Stąd 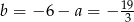 i prosta
i prosta 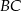 ma równanie
ma równanie 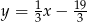 .
.
Prosta zawierająca wysokość opuszczoną z wierzchołka 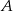 jest prostopadła do prostej
jest prostopadła do prostej 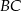 , więc ma równanie postaci
, więc ma równanie postaci 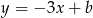 . Współczynnik
. Współczynnik 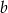 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 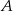 .
.

Wysokość 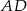 ma więc równanie
ma więc równanie 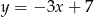 . Szukamy teraz jej punktu wspólnego
. Szukamy teraz jej punktu wspólnego 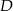 z prostą
z prostą 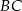 .
.
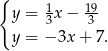
Porównujemy 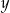 -ki i mamy
-ki i mamy
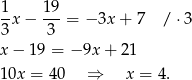
Stąd 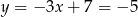 i
i 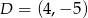 .
.
Odpowiedź: