Zadanie nr 2826020
Funkcja 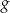 jest określona w zbiorze wszystkich liczb rzeczywistych w następujący sposób: jeśli
jest określona w zbiorze wszystkich liczb rzeczywistych w następujący sposób: jeśli 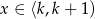 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej  , to
, to 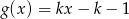 .
.
- Narysuj wykres funkcji
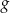 w przedziale
w przedziale 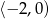 .
. - Uzasadnij, że funkcja
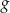 nie ma miejsc zerowych.
nie ma miejsc zerowych. - Rozwiąż równanie
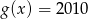 .
.
Rozwiązanie
- Najważniejsze w tym zadaniu to wyobrazić sobie jak funkcja
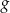 wygląda. Należy sobie o niej myśleć jak o kawałkach prostych na kolejnych przedziałach
wygląda. Należy sobie o niej myśleć jak o kawałkach prostych na kolejnych przedziałach 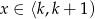 , np. mamy
, np. mamy 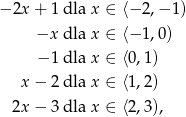
itd.
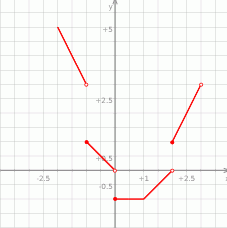
Narysowaliśmy wykres na większym przedziale niż jest w poleceniu (żeby było lepiej widać o co chodzi), aby mieć odpowiedź do polecenia, trzeba oczywiście zmazać wszystko na prawo od 0.
- Powyższy rysunek sugeruje rozwiązanie. Dla
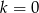 i
i 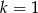 sprawdzamy ze wzoru, że nie ma miejsc zerowych.Dla pozostałych wartości
sprawdzamy ze wzoru, że nie ma miejsc zerowych.Dla pozostałych wartości 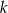 pokażemy, że wartości
pokażemy, że wartości 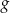 są dodatnie. Jeżeli
są dodatnie. Jeżeli 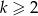 to
to 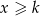 i mamy
i mamy 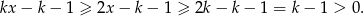
Jeżeli
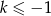 to
to 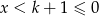 i
i 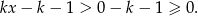
- Liczymy
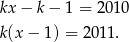
Jeżeli
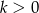 , to z nierówności
, to z nierówności 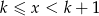 mamy
mamy 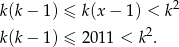
Jedyną liczbą
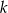 , która spełnia tę nierówność jest
, która spełnia tę nierówność jest 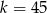 . Wtedy
. Wtedy 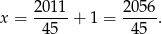
Jeżeli natomiast
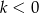 , to podobnie jak poprzednio
, to podobnie jak poprzednio 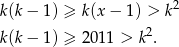
Łatwo się przekonać, że nie ma takiej liczby całkowitej
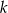 (prawa strona wymusza
(prawa strona wymusza 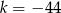 , ale wtedy lewa strona jest za mała).
, ale wtedy lewa strona jest za mała).
Odpowiedź: