Zadanie nr 9942522
Funkcja 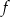 jest funkcją okresową o okresie podstawowym równym
jest funkcją okresową o okresie podstawowym równym 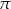 . W przedziale
. W przedziale 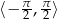 funkcja określona jest wzorem
funkcja określona jest wzorem
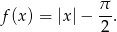
- Wyznacz miejsca zerowe funkcji
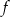 .
. - Podaj zbiór wartości funkcji
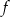 .
. - Oblicz
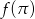 oraz
oraz 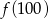 , przyjmując
, przyjmując 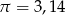 .
. - Naszkicuj wykres funkcji
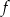 w przedziale
w przedziale 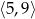 .
.
Rozwiązanie
- O funkcji
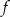 należy mysleć następująco. Na przedziale
należy mysleć następująco. Na przedziale 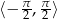 jest to wartość bezwględna
jest to wartość bezwględna 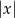 przesunięta o
przesunięta o 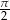 w dół, potem ten wykres kopiujemy w prawo i lewo z przesunięciem o
w dół, potem ten wykres kopiujemy w prawo i lewo z przesunięciem o 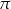 – lewy wykres.
– lewy wykres. 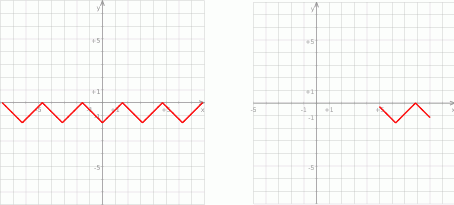
W szczególności miejsca zerowe to
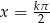 .
.
Odpowiedź: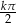 ,
, 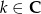
- Jest jasne z poprzedniego podpunktu, że zbiór wartości to
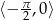 .
.
Odpowiedź: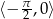
- Liczymy
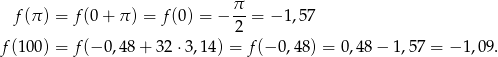
Odpowiedź: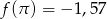 ,
, 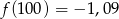
- Trzeba obciąć wykres z pierwszego podpunktu do przedziału
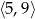 (prawy wykres).
(prawy wykres).

