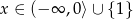/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3/Z parametrem

Zadanie nr 3016428

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 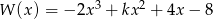3 2 W (x) = − 2x + kx + 4x − 8 .

  • Wyznacz wartość 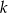k tak, aby reszta z dzielenia wielomianu W przez dwumian 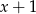x + 1 była równa -6.
  • Dla znalezionej wartości 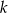k rozłóż wielomian na czynniki liniowe.
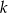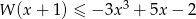  • Dla znalezionej wartości k rozwiąż nierówność W (x + 1) ≤ − 3x 3 + 5x − 2 .

Rozwiązanie

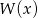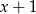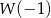  • Reszta z dzielenia W (x) przez dwumian x+ 1 to W (−1 ) . Mamy zatem równanie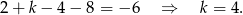
    2 + k− 4− 8 = − 6 ⇒ k = 4 .

     
    Odpowiedź: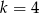 k = 4

  • Dla 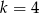k = 4 mamy wielomian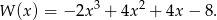
    W (x) = − 2x 3 + 4x 2 + 4x− 8.

    Sprawdzając dzielniki wyrazu wolnego, łatwo zauważayć, że 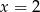x = 2 jest jego pierwiastkiem. Zatem dzielimy przez 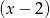(x − 2) . My zrobimy to grupując wyrazy.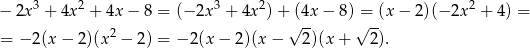

    3 2 3 2 2 − 2x + 4x + 4x − 8 = (−2x + 4x )+ √(4x − 8)√=-(x − 2)(− 2x + 4 ) = = − 2(x − 2)(x 2 − 2 ) = − 2(x− 2)(x − 2)(x + 2).

     
    Odpowiedź: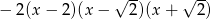 √ -- √ -- − 2(x − 2)(x − 2)(x + 2 )

  • Liczymy
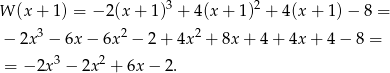
    W (x + 1) = − 2 (x + 1)3 + 4 (x+ 1)2 + 4 (x+ 1)− 8 = 3 2 2 − 2x − 6x − 6x − 2 + 4x + 8x + 4 + 4x + 4− 8 = = − 2x3 − 2x2 + 6x − 2 .

    Musimy więc rozwiązać nierówność

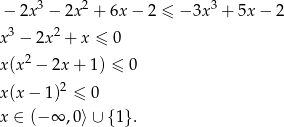
    − 2x3 − 2x2 + 6x − 2 ≤ − 3x3 + 5x − 2 3 2 x − 2x + x ≤ 0 x(x 2 − 2x + 1) ≤ 0 2 x(x − 1 ) ≤ 0 x ∈ (− ∞ ,0⟩ ∪ {1}.

     
    Odpowiedź: x ∈ (− ∞ ,0⟩ ∪ {1}

Wersja PDF