/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3/Z parametrem

Zadanie nr 6824977

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 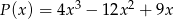3 2 P(x) = 4x − 12x + 9x , gdzie x ∈ R .

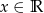  • Dla jakich argumentów wielomian 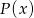P(x) przyjmuje wartość równą 27?
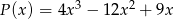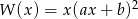  • Wielomiany P (x) = 4x 3 − 12x 2 + 9x oraz W (x) = x(ax + b)2 są równe. Wyznacz a i b .

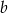Rozwiązanie

  • Liczymy
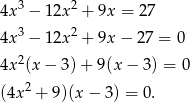
    4x3 − 12x2 + 9x = 27 3 2 4x − 12x + 9x − 27 = 0 4x2(x − 3) + 9(x − 3) = 0 (4x2 + 9)(x − 3) = 0.

    Równanie 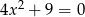2 4x + 9 = 0 nie ma rozwiązań, więc jedynym rozwiązaniem powyższego równania jest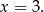

    x = 3.

    Możemy sprawdzić, czy się nie pomyliliśmy

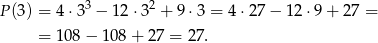
    3 2 P(3) = 4 ⋅3 − 12 ⋅3 + 9⋅ 3 = 4 ⋅27− 12 ⋅9+ 27 = = 1 08− 108 + 27 = 2 7.

     
    Odpowiedź: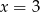 x = 3

  •  

    Sposób I

    Zauważmy, że

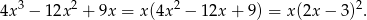
    4x 3 − 12x2 + 9x = x(4x2 − 12x + 9) = x(2x − 3)2.

    W takim razie równość

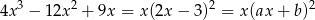
    4x3 − 12x 2 + 9x = x(2x − 3 )2 = x(ax + b)2

    jest spełniona tylko, gdy

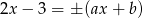
    2x − 3 = ± (ax + b)

    czyli, gdy 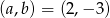(a,b) = (2,− 3) lub (a,b) = (− 2,3) .

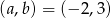    Sposób II

    Rozwińmy najpierw wielomian W

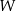
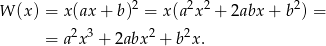
    W (x ) = x(ax + b)2 = x(a2x2 + 2abx + b2) = 2 3 2 2 = a x + 2abx + b x .

    Dwa wielomiany są równe jeżeli współczynniki przy odpowiadających sobie potęgach są równe. Otrzymujemy więc układ równań

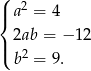
    ( 2 |{ a = 4 2ab = − 12 |( 2 b = 9 .

    Z pierwszego równania otrzymujemy, że

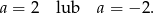
    a = 2 lub a = −2 .

    Podobnie z trzeciego mamy

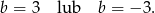
    b = 3 lub b = −3 .

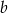    Natomiast drugie równanie mówi nam, że a i b muszą być przeciwnych znaków. Zatem rozwiązaniami są pary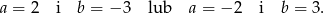

    a = 2 i b = − 3 lub a = − 2 i b = 3.

     
    Odpowiedź: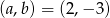 (a,b) = (2,− 3) lub (a,b) = (− 2,3)

Wersja PDF