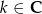/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 3316210

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 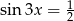1 sin3x = 2 .

Rozwiązanie

Należy naszkicować sobie wykres sinusa i ustalić kiedy przyjmuje on podaną wartość.

PIC

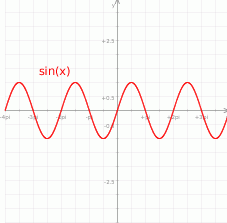
Aby rozwiązać równanie 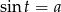sint = a znajdujemy najpierw kąt ostry α , który spełnia to równanie (np. z tablic), wtedy wszystkie rozwiązania są postaci

t = α + 2kπ ∨ t = π − α + 2kπ,

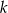gdzie k dowolna liczba całkowita.

Rozwiązaniem równania 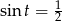1 sin t = 2 są liczby

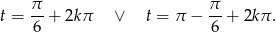
π- π- t = 6 + 2kπ ∨ t = π − 6 + 2k π.

U nas 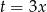t = 3x , zatem

3x = π- + 2kπ ∨ 3x = 5π-+ 2kπ 6 6 π 2kπ 5π 2kπ x = ---+ ---- ∨ x = ---+ ----. 18 3 18 3

 
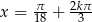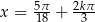Odpowiedź: π- 2kπ- x = 18 + 3 lub 5π- 2kπ x = 18 + 3 , gdzie k ∈ C

Wersja PDF