/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 3503058

Sinus kąta ostrego jest dwa razy większy od cosinusa tego kąta. Wyznacz wartość cosinusa tego kąta i podaj przybliżoną wartość tego kąta.

Wersja PDF

Rozwiązanie

Podane w treści informacje prowadzą do równania

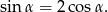
sin α = 2 cos α.

Obie strony są dodatnie (bo kąt jest ostry), więc możemy ją podnieść stronami do kwadratu.

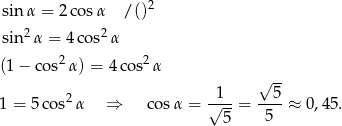
2 sinα = 2cos α / () sin2α = 4cos2 α 2 2 (1− co s α) = 4 cos α √ -- 1 = 5co s2α ⇒ cosα = √1--= --5-≈ 0 ,45. 5 5

Odczytujemy z tablic, że 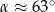α ≈ 63∘ .  
Odpowiedź: 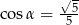√- cosα = -5- 5 , α ≈ 63 ∘

Wersja PDF