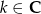/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 3857186

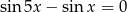Wyznacz wszystkie liczby rzeczywiste x , spełniające równanie sin 5x − sin x = 0 .

Wersja PDF

Rozwiązanie

Sposób I

Korzystamy ze wzoru na różnicę sinusów

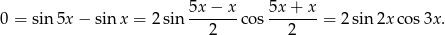
0 = sin5x − sin x = 2 sin 5x-−--xco s 5x-+-x = 2 sin 2x cos3x . 2 2

Zatem

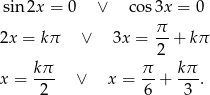
sin2x = 0 ∨ cos 3x = 0 π 2x = kπ ∨ 3x = --+ kπ 2 x = kπ- ∨ x = π-+ kπ-. 2 6 3

Sposób II

Korzystamy z następującej równoważności

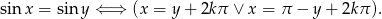
sin x = sin y ⇐ ⇒ (x = y + 2k π ∨ x = π − y+ 2kπ ).

Korzystając z powyższego warunku mamy

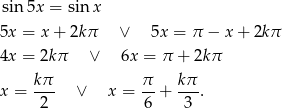
sin5x = sinx 5x = x + 2k π ∨ 5x = π − x + 2k π 4x = 2kπ ∨ 6x = π + 2kπ x = kπ- ∨ x = π-+ kπ-. 2 6 3

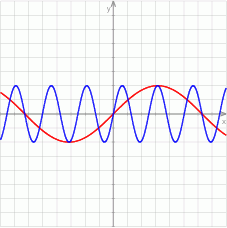
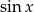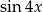Na koniec, dla ciekawskich, wykresy sinx i sin4x (szukaliśmy punktów wspólnych tych wykresów).

PIC

 
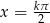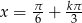Odpowiedź: x = k2π- lub x = π6-+ k3π- , k ∈ C

Wersja PDF